
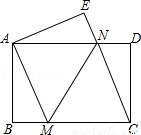
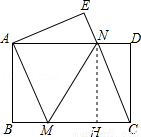
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.
(1)证明见解析;(2)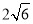 .
.
【解析】
试题分析:(1)由折叠的性质可得:∠ANM=∠CNM,由四边形ABCD是矩形,可得∠ANM=∠CMN,则可证得∠CMN=∠CNM,继而可得CM=CN.
(2)首先过点N作NH⊥BC于点H,由△CMN的面积与△CDN的面积比为3:1,易得MC=3ND=3HC,然后设DN=x,由勾股定理,可求得MN的长.
(1)由折叠的性质可得:∠ANM=∠CNM .
∵ 四边形ABCD是矩形,
∴ AD∥BC .
∴ ∠ANM=∠CMN .
∴ ∠CMN=∠CNM .
∴ CM=CN.
(2)如图,过点N作NH⊥BC于点H,则四边形NHCD是矩形.
∴HC=DN,NH=DC.
∵ △CMN的面积与△CDN的面积比为3:1,
∴ MC=3ND=3HC.
∴ MH=2HC.
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN.
在Rt△CDN中,DC=2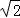 x=4,
x=4,
∴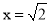 .
.
∴HM=2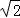 .
.
在Rt△MNH中,MN=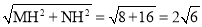 .
.
考点:1.翻折变换(折叠问题);2.矩形的性质;3.等腰三角形的判定;4.三角形的面积;5.勾股定理.


科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
已知抛物线 ,
,
(1)若 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;
(3)若 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
某中学书法兴趣小组12名成员的年龄情况如下:
年龄(岁) | 12 | 13 | 14 | 15 | 16 |
人数 | 1 | 4 | 3 | 2 | 2 |
则这个小组成员年龄的众数和中位数分别是( )
A.15,16 B.13,14 C.13,15 D.14,14
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
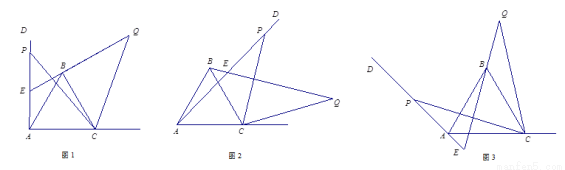
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:选择题
若二次函数y=x2﹣2x+c的图象与y轴的交点为(0,﹣3),则此二次函数有( )
A.最小值为-2 B.最小值为-3 C.最小值为-4 D.最大值为-4
查看答案和解析>>
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:填空题
甲、乙、丙三人分别拿出相同数量的钱,合伙订购某种商品若干件.商品买来后,甲、乙分别比丙多拿了7、11件,最后结算时,三人要求按所得商品的实际数量付钱,进行多退少补.已知甲要付给丙14元, 那么乙还应付给丙 元.
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )
A.(x+2)2=9 B.(x﹣2)2=9 C.(x+2)2=1 D.(x﹣2)2=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com