
已知抛物线 ,
,
(1)若 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;
(3)若 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.
(1)(-1,0)和(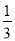 ,0);(2)证明见解析;(3)3或
,0);(2)证明见解析;(3)3或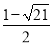 .
.
【解析】
试题分析:(1)将a、b、c的值代入,可得出抛物线解析式,从而可求解抛物线与x轴的交点坐标.
(2)把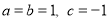 代入抛物线解析式,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论.
代入抛物线解析式,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论.
(3)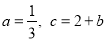 ,则抛物线可化为
,则抛物线可化为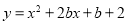 ,其对称轴为x=-b,以-1≤x≤2为区间,讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
,其对称轴为x=-b,以-1≤x≤2为区间,讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
(1)当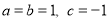 时,抛物线为
时,抛物线为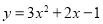 ,
,
∵方程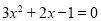 的两个根为x1=-1,x2=
的两个根为x1=-1,x2=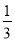 ,
,
∴该抛物线与x轴交点的坐标是(-1,0)和(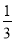 ,0).
,0).
(2)当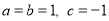 时,抛物线
时,抛物线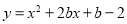 ,
,
设y=0,则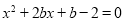 ,
,
∴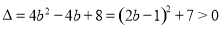 ,
,
∴抛物线与x轴有两个交点.
(3)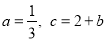 ,则抛物线可化为
,则抛物线可化为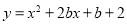 ,其对称轴为x=-b,
,其对称轴为x=-b,
当-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,
此时-3=(-2)2+2×(-2)b+b+2,
解得:b=3,符合题意.
当-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,
此时-3=22+2×2b+b+2,
解得:b=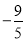 ,不合题意,舍去.
,不合题意,舍去.
当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b1=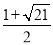 (不合题意,舍去),b2=
(不合题意,舍去),b2= .
.
综上可得:b=3或b=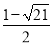 .
.
考点:1.抛物线与x轴的交点;2.二次函数的最值;3.分类思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
为保证“燕房线”轻轨建设,我区对一条长2 500米的道路进行改造.在改造了1 000米后,为了减少施工对交通造成的影响,采用了新的施工工艺,使每天的工作效率是原来的1.5倍,结果提前5天完成任务.求原来每天改造道路多少米?
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:选择题
党中央、国务院从扩大就业等方面保障和增加居民收入,据统计2013年,全国城镇新增就业人数1310万人,将1310用科学计数法表示应为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
在一个口袋中,装有质地、大小均相同、颜色不同的红球3个,蓝球4个,黄球5个,现在随机抽取一个球是红球的概率是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
某酒店有三人间、双人间的客房,三人间每天每间150元,双人间每人每天140元,为了吸引游客, 实行团体入住五折优惠措施,一个50人的旅游团优惠期间到该酒店入住,住了一些三人间和双人间客房,若每间客房正好住满且一天共花去住宿费1510元,则该旅行团住了三人间和双人间客房各多少间?
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
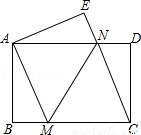
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:选择题
下列事件中,必然事件是 ( )
A.掷一枚硬币,正面朝上.
B.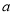 是有理数,则
是有理数,则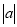 ≥0.
≥0.
C.某运动员跳高的最好成绩是20 .1米.
D.从车间刚生产的产品中任意抽取一个,是次品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com