
问题:在△ABC中,AB=AC,∠A=100°,BD为∠B 的平分线,探究AD、BD、BC之间的数量关系.
请你完成下列探究过程:
(1)观察图形,猜想AD、BD、BC之间的数量关系为 .
(2)在对(1)中的猜想进行证明时,当推出∠ABC=∠C=40°后,可进一步推出∠ABD=∠DBC= 度.
(3)为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在BC上截取BE=BD,连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.
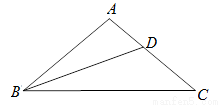
(1)AD+BD=BC;(2)20;(3)证明见解析.
【解析】
试题分析:在BC上截取BE=BD,在BC上截取BF=BA,连接DF,通过证明△ABD≌△FBD得到AD=DF,应用等腰三角形的判定和性质,三角形内角和定理得到∠DBC=20°和AD+BD=BC.
试题解析:(1)AD+BD=BC.
(2)20.
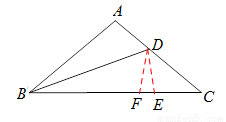
(3)画出图形,证明如下:
在BC上截取BF=BA,连接DF,
∵∠ABD=∠DBC,BD=BD,∴△ABD≌△FBD.∴AD=DF.
∵∠A=100°,∴∠DFB=∠A=100°,∴∠DFC=80°.
∵BE=BD,∠DBC=20°, ∴∠BED =∠BDE =80°,∠DFE =∠FED.
∴DF=DE.
∵∠FED=80°,∠C=40°,∴∠EDC=40°.
∴∠EDC =∠C,∴DE =EC.
∴AD =EC,∴AD+BD=BC.
考点:1.探究型问题;2.全等三角形的判定和性质;3.等腰三角形的判定和性质;4.三角形内角和定理.


科目:初中数学 来源:2014年北京市海淀区中考二模数学试卷(解析版) 题型:解答题
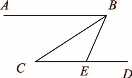
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF= ,求△CAF的面积.
,求△CAF的面积.

查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:选择题
若正多边形的一个外角是36°,则该正多边形为( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:填空题
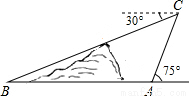
如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A,B两点间的距离为 米.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:选择题
如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,则∠1+∠2等于( )

A.30° B.40° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:填空题
已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第4个图形中直角三角形的个数有________________个;第2014个图形中直角三角形的个数有_________________个.

查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
(1)求证:AC=CD.
(2)若AC=2,AO= ,求OD的长.
,求OD的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
如图,已知AB∥CD,BC平分∠ABE,∠C= ,则∠BED 的度数是( )
,则∠BED 的度数是( )
A.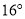 B.
B. C.
C.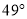 D.
D.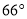
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com