
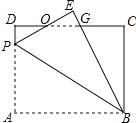
【题目】如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为_____.

【答案】2.4
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=4,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=3﹣x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
解:如图所示:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=3,CD=AB=4,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=4,
在△ODP和△OEG中,
 ,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=3﹣x,DG=x,
∴CG=4﹣x,BG=4﹣(3﹣x)=1+x,
根据勾股定理得:BC2+CG2=BG2,
即32+(4﹣x)2=(x+1)2,
解得:x=2.4,
∴AP=2.4;
故答案为:2.4.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.去年当地每月的平均气温如图1,小明家去年月用电量如图2.

根据统计图,回答下面的问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .动点
.动点![]() 从点
从点![]() 出发,按
出发,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() ,设出发时间为
,设出发时间为![]() .
.

(1)求![]() 的长.
的长.
(2)当![]() 时,求证:
时,求证:![]() .
.
(3)当点![]() 在
在![]() 边上运动时,若
边上运动时,若![]() 是以
是以![]() 为腰的等腰三角形,求出所有满足条件的
为腰的等腰三角形,求出所有满足条件的![]() 的值.
的值.
(4)在整个运动过程中,若![]() (
(![]() 为正整数),则满足条件的
为正整数),则满足条件的![]() 的值有________个.
的值有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕.若AB=3,BC=9.点D对应点是G.

(1)求BE长;
(2)求EF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.

(1)请你写出图中所有的等腰三角形;
(2)请你判断AD与BE垂直吗?并说明理由.
(3)如果BC=10,求AB+AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com