
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=![]() ,求BE的长.
,求BE的长.

【答案】(1)证明见解析;(2)3.2.
【解析】试题分析:(1)连接DO,由等腰三角形的性质和角平分线的定义得出∠1=∠3,证出DO∥BC,由平行线的性质得出∠ADO=90°,即可得出结论;
(2)设⊙O的半径为R,由三角函数求出BC,由平行线得出△AOD∽△ABC,得出对应边成比例,求出半径OD,过O作OF⊥BC于F,则BE=2BF,如图所示:则OF∥AC,由平行线的性质得出∠BOF=∠BAC,由三角函数求出BF,即可得出结果.
试题解析:(1)连接DO,如图1所示
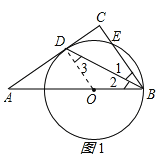
∵BD是∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠2=∠3,
∴∠1=∠3,
∴DO∥BC,
∵∠C=90°,
∴∠ADO=90°,
即AC⊥OD,
∴AC是⊙O的切线.
(2)设⊙O的半径为R,
在Rt△ABC中,∠ACB=90°,sin∠BAC=![]() ,
,
∴BC=![]() ×6=4,
×6=4,
由(1)知,OD∥BC,
∴△AOD∽△ABC,
∴![]() ,
,
∴![]() ,
,
解得:R=2.4,
过O作OF⊥BC于F,如图所示:
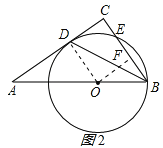
则BE=2BF,OF∥AC,
∴∠BOF=∠BAC,
∴![]() sin∠BOF=
sin∠BOF=![]() ,
,
∴BF=![]() ×2.4=1.6,
×2.4=1.6,
∴BE=2BF=3.2.


科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”
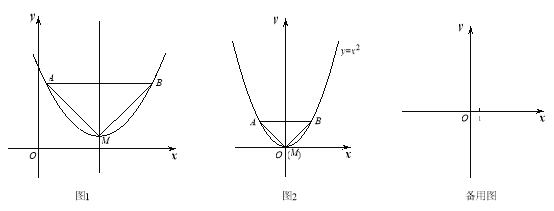
(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
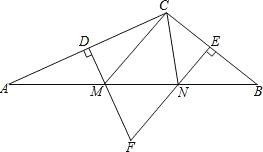
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3
B.三边长的平方之比为1:2:3
C.三边长之比为3:4:5
D.三内角之比为3:4:5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com