
����Ŀ�����ųǼ���·����ʽ��ͨ���Ӽ��о����е����еĸ�����̱��տ����������90km������ʱ�������8h����֪���е����е��տ��г����Ϊ1220km������ƽ��ʱ�����տ�ƽ��ʱ�ٵ�2.5����
��1��������г���ƽ��ʱ�٣�
��2��ij��������Ҫ�Ӽ���ȥ�����Լ780km�ı��вμ�14��00�ٿ��Ļ��飬���������9��20�Ӽ��е����еĸ���Ʊ�����Ҵӱ��л�վ������ص������Ҫ1Сʱ�������ڸ����г��㵽�������£����ܷ��ڿ���֮ǰ20���Ӹϵ�����ص㣿
���𰸡�
��1���⣺���տ��ƽ��ʱ��Ϊxǧ��/Сʱ�������г���ƽ��ʱ��Ϊ2.5xǧ��/Сʱ��
������ã� ![]() ��
�� ![]() =8��
=8��
��ã�x=96��
�����飬x=96��ԭ��ʽ���̵Ľ⣬�ҷ������⣬
��2.5x=240��
�𣺸����г���ƽ��ʱ��Ϊ240ǧ��/Сʱ
��2���⣺780��240=3.25��
����������Ҫ3.25+1=4.25��Сʱ����
��9��20������1��40������4 ![]() Сʱ��4.25Сʱ��
Сʱ��4.25Сʱ��
�����������ڿ���֮ǰ����
����������1�����տ��ƽ��ʱ��Ϊxǧ��/Сʱ�������г���ƽ��ʱ��Ϊ2.5xǧ��/Сʱ����������ɵã������ߣ�1220��90��ǧ�ױ��տ���1220ǧ��ʱ�������8Сʱ���ݴ��з�����⣻��2��������������õ�ʱ�䣬Ȼ������жϣ�
�����㾫�������ڱ��⿼��ķ�ʽ���̵�Ӧ�ã���Ҫ�˽��з�ʽ���̽�Ӧ����IJ��裺���⡢��δ֪��������ȹ�ϵ�з��̡��ⷽ�̲������д���𰸣�Ҫ�е�λ�����ܵó���ȷ�𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
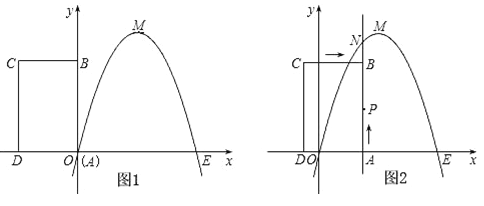
����Ŀ����ͼ����֪�����߾�������ԭ��O��x������һ��E������M������Ϊ��2��4��������ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
��1���������������Ӧ�ĺ�����ϵʽ��
��2��������ABCD��ÿ��1����λ���ȵ��ٶȴ���ͼ��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��3����ֱ��AB��������ߵĽ���ΪN����ͼ2��ʾ����
�ٵ�t=![]() ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
������P��N��C��DΪ����Ķ�������ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
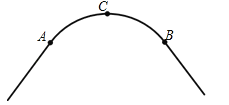
����Ŀ����ͼ��һ����·��ת�䴦��һ��Բ����![]() ����
����
��1����ֱ�ߺ�Բ������![]() ����Բ��Բ��O����Ҫ������ͼ�ۼ�����д������
����Բ��Բ��O����Ҫ������ͼ�ۼ�����д������
��2����![]() ���е�C����AB�ľ���Ϊ20m��AB=80m����
���е�C����AB�ľ���Ϊ20m��AB=80m����![]() ����Բ�İ뾶��
����Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����֣���ͼ�٣��ڡ�ABC�У���ACB=2��B����ACB=90�㣬ADΪ��BAC��ƽ���ߣ��ҽ�BC��D�����Ƿ�����AB�Ͻ�ȡAE=AC������DE���ɵ�AB=AC+CD������֤������ 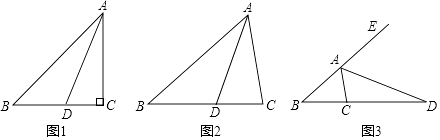
��1��̽������ͼ�ڣ�����ACB��90��ʱ�������������䣬�߶�AB��AC��CD����������������ϵ��д���������֤����
��2����չ����ͼ�ۣ�����ACB=2��B����ACB��90��ʱ��ADΪ��ABC����ǡ�CAF��ƽ���ߣ��ҽ�BC���ӳ����ڵ�D�����߶�AB��AC��CD����������������ϵ��д����IJ��룬����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����A=��ADE����C=��E��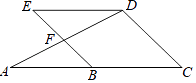
��1������EDC=3��C�����C�Ķ�����
��2����֤��BE��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������µ����߷ֱ�ƽ�У������� =��x+10���㣬���� =��2x��25���㣬�������Ķ���Ϊ�� ��
A��45�� B��75�� C��45����75�� D��45����55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��ADƽ�֡�BAC��DE��AB��DF��AC��E��FΪ���㣬�������ĸ����ۣ���1����DEF=��DFE����2��AE=AF����3��ADƽ�֡�EDF����4��EF��ֱƽ��AD��������ȷ���У� �� 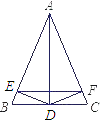
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�������dz����ĵ�ש�ϵ�ͼ�������а�����һ�������ƽ��ͼ�Ω����˱��Σ�
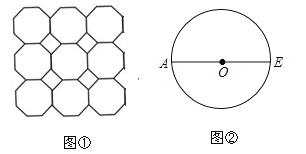
��1����ͼ�ڣ�AE�ǡ�O��ֱ������ֱ�ߺ�Բ������O���ڽ����˱���ABCDEFGH����д������������ͼ�ۼ�����
��2���ڣ�1����ǰ���£�����OD����֪OA=5��������OAD����AOD��180�㣩��һ��Բ�IJ��棬�����Բ����Բ�İ뾶���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϵ�-1��ľ������1����λ�ĵ�����ʾ������
A. 0 B. -1 C. 1��-2 D. 0��-2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com