
【题目】已知(a+b)2=11,(a—b)2=7,求a2+b2与ab的值.
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50 km为标准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50 km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
(1)请求出这七天中平均每天行驶多少千米?
(2)若每天行驶100 km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
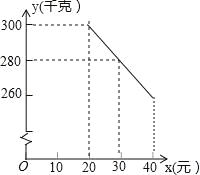
【题目】(2016云南省第22题)草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式(也称关系式)
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
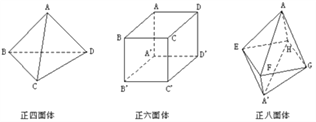
【题目】仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
查看答案和解析>>
科目:初中数学 来源: 题型:
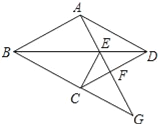
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省岳阳市第24题)如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com