
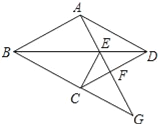
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列方程中两个实数根的和等于2的方程是( )
A.2x2﹣4x+3=0
B.2x2﹣2x﹣3=0
C.2y2+4y﹣3=0
D.2t2﹣4t﹣3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:①等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合;②有两边和其中一边的对角分别相等的两个三角形全等;③三角形的三条高不一定有交点.其中属于真命题的是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的.如图所示是该市自来水收费价格见价目表.
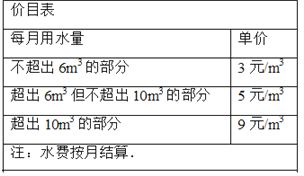
(1)填空:若该户居民2月份用水4m3,则应收水费 元;
(2)若该户居民3月份用水am3(其中6<a<10),则应收水费多少元?(用a的整式表示并化简)
(3)若该户居民4,5月份共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4,5月份共交水费多少元?(用x的整式表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b) 米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=10,b=8,且每平方米造价为100元求出绿化需要多少费用.
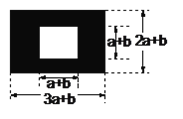
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com