
����Ŀ����ͼ1��ƽ��ֱ������ϵxOy�У���A��0��4����B��1��0������ABΪֱ�DZ�������Rt��ABC����CAB��90�㣬AB��AC��

��1����ͼ1����C�����ꣻ
��2����ͼ2����ͼ1�й�C����CD��x����D������AD�����ADC�Ķ�����
��3����ͼ3����A��y�����˶�����OAΪֱ�DZ�������Rt��OAE������EC����y����F������A�����˶�������S��AOB��S��AEF��ֵ�Ƿ�ᷢ���仯�����û�б仯����˵�����ɣ�
���𰸡���1��C��4��5������2��45�㣻��3��A�����˶�������S��AOB��S��AEF��ֵ���ᷢ���仯�����ɼ�����
��������
��1�����жϡ�AOB�ա�CGA�����CE��OA��4��AG��OB��1�����ɵó����ۣ�
��2���ɣ�1��֪C��4��5���������OD��4������OA��OD���ó���OAD��45�㣬�����ƽ���ߵ����ʼ��ɵó����ۣ�
��3�����жϵ�E��y�����࣬�ٷֵ�A��y��������������ϣ�ͬ��1���ķ��������C���꣬�ô���ϵ�������ֱ��CE�Ľ���ʽ�����������F�����꣬���ɵó����ۣ�
��1����ͼ����
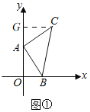
��A��0��4����B��1��0����
��OA��4��OB��1������C��CG��y����G��
���AGC��90�㣽��BOA��
���OAB+��OBA��90��
�ߡ�CAB��90�㣬
���OAB+��GAC��90�㣬
���OBA����GAC��
��AB��AC��
���AOB�ա�CGA��AAS����
��CG��OA��4��AG��OB��1��
��OG��OA+AG��5��
��C��4��5����
��2���ɣ�1��֪��OA��4����C��4��5����
��CD��x�ᣬ
���D��4��0����
��OD��4��
��OA��OD��
��OAD��45�㣬
��CD��x�ᣬ
��CD��y�ᣬ
���ADC����OAD��45�㣻
��3��A�����˶�������S��AOB��S��AEF��ֵ���ᷢ���仯��
���ɣ����A������Ϊ��0��a����
������A��y����������ʱ������CE��y����F��
���C��E��y������࣬����E��y����࣬
ͬ��1���ķ����ã�C��a��a+1����
�ߡ�OAE�ǵ���ֱ�������Σ�
��AE��OA��
��E����a��a����
��ֱ��CE�Ľ���ʽΪy��![]() x+a+
x+a+![]() ��
��
��F��0��a+![]() ����
����
��AF��a+![]() -a��
-a��![]() ��
��
��OB��1��
��![]() =
=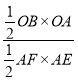 =
=![]() =
=![]() ��2��
��2��
������A��y�Ḻ������ʱ��ͬ���ķ����ã�C����a��a��1����E��a��a����
��ֱ��CE�Ľ���ʽΪy��![]() x+a-
x+a-![]() ��
��
��F��0��a-![]() ����
����
��AF��![]() ��
��
���![]() =
=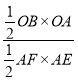 =
=![]() =
=![]() ��2��
��2��
��A�����˶�������S��AOB��S��AEF��ֵ���ᷢ���仯��


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
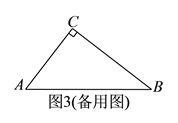
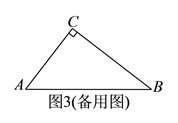
����Ŀ����ͼ����֪�ȱ���ABC�У�D��AC���е㣬E��BC�ӳ����ϵ�һ�㣬��CE=CD��DM��BC������ΪM��
��1�����E�Ķ�����
��2����֤��M��BE���е㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г����쳧������һ����ʽ���г����ƻ�![]() �·�������װ
�·�������װ![]() �������ڳ�������㹻���������������ʽ���г��İ�װ������������ƸһЩ�¹��ˣ����Ǿ�����ѵ��Ҳ�ܶ������а�װ.���в��ŷ��֣�
�������ڳ�������㹻���������������ʽ���г��İ�װ������������ƸһЩ�¹��ˣ����Ǿ�����ѵ��Ҳ�ܶ������а�װ.���в��ŷ��֣� ![]() ����������
����������![]() ���¹���ÿ�տɰ�װ�����г���
���¹���ÿ�տɰ�װ�����г��� ![]() ����������
����������![]() ���¹���ÿ�տɰ�װ
���¹���ÿ�տɰ�װ![]() �����г���
�������
(1)ÿ�����������¹���ÿ�շֱ����װ���������г���
(2)���������Ƹ![]() ���¹���(
���¹���(![]() ).ʹ����Ƹ���¹��˺ͳ���������պ������
).ʹ����Ƹ���¹��˺ͳ���������պ������![]() �·�(
�·�(![]() ��)�İ�װ������ô�������ļ����¹��˵���Ƹ������
��)�İ�װ������ô�������ļ����¹��˵���Ƹ������
(3)�����г�������̥��ʹ��������˵��������̥�簲װ��ǰ�֣���ȫ��ʹ·��Ϊ![]() ǧ����簲װ�ں��֣���ȫ��ʹ·��Ϊ
ǧ����簲װ�ں��֣���ȫ��ʹ·��Ϊ![]() ǧ����.����һ����̥����ʹ���·���Ƕ���ǧ���
ǧ����.����һ����̥����ʹ���·���Ƕ���ǧ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �֣���ͼ����
�֣���ͼ����![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() �ڱ�
�ڱ�![]() ���˶���
���˶��� ![]() ƽ��
ƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
��


��![]() ����
����![]() ʱ����֤��
ʱ����֤�� ![]() ��
��
��![]() ��̽����
��̽���� ![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]() ��
��![]() ���ƣ�
���ƣ�
��![]() ��ֱ��д����
��ֱ��д���� ![]() __________ʱ���ı���
__________ʱ���ı���![]() ��
��![]() �������ȣ�
�������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �֣���ͼ����
�֣���ͼ����![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() �ڱ�
�ڱ�![]() ���˶���
���˶��� ![]() ƽ��
ƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
��


��![]() ����
����![]() ʱ����֤��
ʱ����֤�� ![]() ��
��
��![]() ��̽����
��̽���� ![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]() ��
��![]() ���ƣ�
���ƣ�
��![]() ��ֱ��д����
��ֱ��д���� ![]() __________ʱ���ı���
__________ʱ���ı���![]() ��
��![]() �������ȣ�
�������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��C��D��B����O��ΪԲ�ģ�OA��Ϊ�뾶��Բ���ϣ� AC=CD=DB��AB��OC�ڵ�E����֤��AE=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������ ABCO���߳��� 4���� D(a��0)���� AD Ϊ����AD ���Ҳ������� Rt��ADE����ADE��90�������� OE���� OE ����СֵΪ__________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ��
��
��1������ kΪ��ֵ������ͼ��ع����㣬��õ�����ꣻ
��2����ͼ 1���� k=-![]() ʱ����ֱ�߽� x �ᣬy ���� A��B ���㣬ֱ�� l2:y=x+1 �� AB �ڵ� P���� Q �� l2 ��һ�㣬�� SABQ 6 ���� Q ������ꣻ
ʱ����ֱ�߽� x �ᣬy ���� A��B ���㣬ֱ�� l2:y=x+1 �� AB �ڵ� P���� Q �� l2 ��һ�㣬�� SABQ 6 ���� Q ������ꣻ
��3����ͼ 2���ڵ� 2 �ʵ������£���֪ D ���ڸ�ֱ���ϣ�������Ϊ 1��C ���� x �Ḻ���ᣬ ABC=45 ������ M ������Ϊ��a��a������ CM+MD ����Сֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com