
【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗![]() 已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.
已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.
![]() 、B两种树苗的单价分别是多少元?
、B两种树苗的单价分别是多少元?
![]() 该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵.
该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵.
【答案】(1)A种树苗单价为60元,B中树苗单为50元;(2)最多可以购进A种树苗15棵.
【解析】(1)设购进A种树苗每棵需要x元,B种树苗每棵需要y元,根据“2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种树苗m棵,则购进B种树苗(28-m)棵,根据总价=单价×购进数量结合总费用不超过1550元,即可得出关于m的一元一次不等式,解之即可得出结论;
![]() 设A种树苗单价为x元,B种树苗单价为y元,
设A种树苗单价为x元,B种树苗单价为y元,
根据题意,得![]() ,
,
解方程组,得![]() ,
,
答:A种树苗单价为60元,B中树苗单为50元.
![]() 设购进A种树苗m棵,则购进B种树苗
设购进A种树苗m棵,则购进B种树苗![]() 棵,
棵,
根据题意,得![]() ,
,
解不等式,得![]() ,
,
因为m为整数,所以m的最大值是15,
答:最多可以购进A种树苗15棵.


科目:初中数学 来源: 题型:
【题目】如图,AC⊥BD 于点 , 是 AB 上一点,FD 交 AC 于点 E,∠B 与 ∠D 互余.

(1)试说明:∠A=∠D;
(2)若 AE=1,AC=CD=2.5,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的进度均保持不变).储运部库存物资w(吨)与时间t(小时)之间的函数关系如图所示,请问这批物资从开始调进到全部调出需要多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( ) 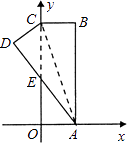
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. 
(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径 ![]() 的长为( )
的长为( ) 
A.π
B.2π
C.4π
D.8π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com