
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2, 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2![]() ,则a的值为________.
,则a的值为________.
【答案】﹣1
【解析】
试题由关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根,根据一元二次方程的二次项系数不为0和根的判别式求出a的取值范围.设抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点坐标分别为(α,0)、(β,0),且α<β,得出α、β是关于x的方程x2﹣(2a+1)x+2a﹣5=0的两个不相等的实数根,由抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别位于点(2,0)的两旁,利用根与系数的关系确定a的取值范围;把|x1|+|x2|=2![]() 变形后,利用根与系数的关系求出a的值.
变形后,利用根与系数的关系求出a的值.
解:∵关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根,
∴![]() 且
且![]() ,
,
解得:a<0,且a≠﹣2 ①
设抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,
则α、β是关于x的方程x2﹣(2a+1)x+2a﹣5=0的两个不相等的实数根,
∵△=[﹣(2a+1)]2﹣4×1×(2a﹣5)=(2a﹣1)2+21>0,
∴a为任意实数②
由根与系数关系得:α+β=2a+1,αβ=2a﹣5.
∵抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别位于点(2,0)的两旁,
∴α<2,β>2,
∴(α﹣2)(β﹣2)<0,
∴αβ﹣2(α+β)+4<0,
∴2a﹣5﹣2(2a+1)+4<0
解得:a>﹣![]() ③
③
由①、②、③得a的取值范围是﹣![]() <a<0;
<a<0;
∵x1和x2是关于x的方程(a+2)x2﹣2ax+a=0的两个不相等的实数根
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∵﹣![]() <a<0,
<a<0,
∴a+2>0,
∴x1x2=![]() <0.
<0.
不妨设x1>0,x2<0,
∴|x1|+|x2|=x1﹣x2=2![]() ,
,
∴x12﹣2x1x2+x22=8,即(x1+x2)2﹣4x1x2=8,
∴(![]() )2﹣
)2﹣![]() =8,
=8,
解这个方程,得:a1=﹣4,a2=﹣1,
经检验,a1=﹣4,a2=﹣1都是方程(![]() )2﹣
)2﹣![]() =8的根.
=8的根.
∵a=﹣4<﹣![]() ,舍去,
,舍去,
∴a=﹣1为所求.
故答案为﹣1.


科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在位于灯塔P的北偏东30°方向,距离灯塔120海里的A处.轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求轮船所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形,他们的周长分别是36和12.周长较大的三角形的最大边为15,周长较小的三角形的最小边为3,则周长较大的三角形的面积是( )
A. 52 B. 54 C. 56 D. 58
查看答案和解析>>
科目:初中数学 来源: 题型:
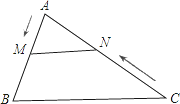
【题目】如图,在△ABC中,AB=6cm, AC=12cm,动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t,使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
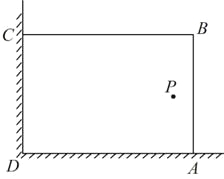
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
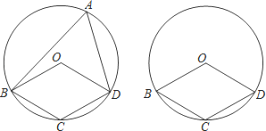
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
(1)若点A在优弧![]() 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com