
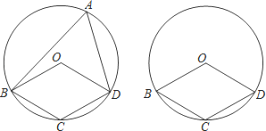
����Ŀ����ͼ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ�����㣨�����B��C��D�غϣ���
��1������A���Ż�![]() �ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
�ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
��2�����ı���OBCDΪƽ���ı��Σ�
�ٵ�Բ��O�ڡ�BAD���ڲ�ʱ�����OBA+��ODA�Ķ�����
�ڵ�Բ��O�ڡ�BAD���ⲿʱ���뻭��ͼ�β�ֱ��д����OBA���ODA��������ϵ��
���𰸡���1��60������2����60�����ڡ�OBA=��ODA+60����
��������
���⣨1������BD������Բ�ܽǶ����������BAD�Ķ����Ƕ��٣�Ȼ����������ε��ڽǺͶ����������0BD����ODB�Ķ������Ƕ��٣��������ABD�У���180����ȥ��BAD����0BD����ODB�Ķ����ͣ������OBA+��ODA���ڶ��ټ��ɣ�
��2�������ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
�����ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
����������⣺��1����ͼ1������BD��
�ߡ�BOD=120����
���BAD=120���2=60����
���0BD+��ODB=180�㩁��BOD=180�㩁120��=60����
���OBA+��ODA=180�㩁����0BD+��ODB������BAD=180�㩁60�㩁60��=120�㩁60��=60����
�ʴ�Ϊ��60��
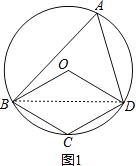
��2������ͼ2��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OBC=��ODC=180�㩁120��=60����
���ߡ�ABC+��ADC=180����
���OBA+��ODA=180�㩁����OBC+��ODC��=180�㩁��60��+60����=180�㩁120��=60����
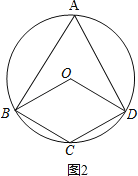
����ͼ3��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OAB=��OAD+��BAD=��OAD+60����
��OA=OD��OA=OB��
���OAD=��ODA����OAB=��OBA��
���OBA=��ODA+60����


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��ֱ��l�ϣ�AB=10cm����B�İ뾶Ϊ1cm����C��ֱ��l�ϣ�����C��ֱ��CD����DCB=30����ֱ��CD��A�������ÿ��4cm���ٶ���������ƽ���˶������ͬʱ����B�İ뾶Ҳ����������뾶r��cm����ʱ��t���룩֮��Ĺ�ϵʽΪr=1+t��t��0������ֱ��CD����________��ֱ��CDǡ������B���У�
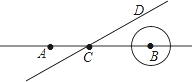
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬EΪBC��һ�㣬��CEΪֱ������O��AB����O�����ڵ�D������CD����BE=OE=2��
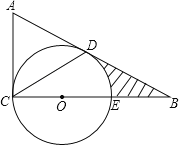
��1����֤����A=2��DCB��
��2����ͼ����Ӱ���ֵ��������������к��ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�a+2��x2��2ax+a=0����������ȵ�ʵ����x1��x2�� ������y=x2����2a+1��x+2a��5��x�����������ֱ�Ϊλ�ڵ㣨2��0�������ԣ���|x1|+|x2|=2![]() ����a��ֵΪ________��
����a��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��A=25�㣬�Ե�CΪԲ�ģ�BCΪ�뾶��Բ��AB�ڵ�D����AC�ڵ�E����![]() �Ķ���Ϊ��������
�Ķ���Ϊ��������
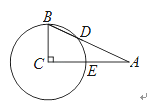
A. 25�� B. 30�� C. 50�� D. 65��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��BC���е㣬��E��F�ֱ����߶�AD�����ӳ����ϣ���DE=DF����������������

��BE��EC����BF��CE����AB=AC��
����ѡ��һ������ʹ�ı���BECF�����Σ�����Ϊ��������� ��ֻ��д��ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�߷�ʱ��37·����������վ�˸�·�����е���������������10����γ˸�·��������������£�16��25��18��27��25��30��28��29��25��27��
(1)�������10����γ˸�·��������ƽ��������������λ����
(2)���37·�������ڸ߷�ʱ�δ���վ������50����Σ���������ļ������������ڸ߷�ʱ�δ���վ�˸�·�����еij˿��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ֽƬ![]() ������������²�����
������������²�����
��![]() ���ۣ�ʹ�õ�
���ۣ�ʹ�õ�![]() ���
���![]() �أ��ۺ�Ϊ
�أ��ۺ�Ϊ![]() ����
����![]() ���ۣ�ʹ�õ�
���ۣ�ʹ�õ�![]() ���
���![]() �غϣ��ۺ�Ϊ
�غϣ��ۺ�Ϊ![]() (��ͼ2)������
(��ͼ2)������![]() ���������ۺ۵��ӳ��߽��ڵ�
���������ۺ۵��ӳ��߽��ڵ�![]() ��
��
(1)����ͼ2�н�ͼ�β�������������![]() �Ķ�����
�Ķ�����
(2)�ı���![]() ��������˵�����ɣ�
��������˵�����ɣ�
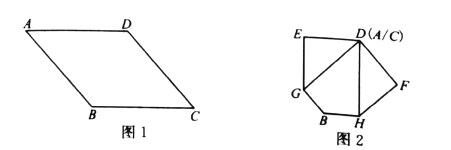
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABOC��AB��AC�ֱ����O�����ڵ�D��E������D��AB���е������DOE=__________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com