
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
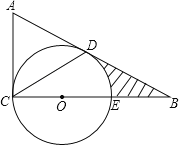
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
【答案】解:(1)证明:连接OD,
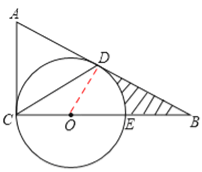
∵AB是⊙O切线,∴∠ODB=90°。
∴BE=OE=OD=2。
∴∠B=30°,∠DOB=60°。
∵OD=OC,∴∠DCB=∠ODC=![]() ∠DOB=30°。
∠DOB=30°。
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°。∴∠A=2∠DCB。
(2)∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2![]() ,
,
∴阴影部分的面积![]()
【解析】
试题(1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案。
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案。


科目:初中数学 来源: 题型:
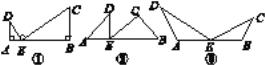
【题目】(1)尝试:如图①,已知A,E,B三点在同一直线上,且∠A=∠B=∠DEC=90°,求证:△ADE∽△BEC;
(2)一名同学在尝试了上题后还发现:如图②、图③,只要A,E,B三点在同一直线上,且∠A=∠B=∠DEC,则(1)中的结论总成立.你同意吗?请选择其中之一说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①![]() =
=![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+![]() .其中正确的是( )
.其中正确的是( )

A. ①③④ B. ①②③ C. ①② D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
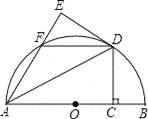
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 | 优惠办法 |
少于200元 | 不予优惠 |
低于500元但不低于200元 | 九折优惠 |
500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(1)王老师一次性购物600元,他实际付款 元.
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款 元,当x大于或等于500元时,他实际付款 元.(用含x的代数式表示).
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的代数式表示:两次购物王老师实际付款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com