
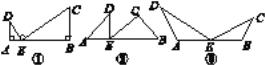
【题目】(1)尝试:如图①,已知A,E,B三点在同一直线上,且∠A=∠B=∠DEC=90°,求证:△ADE∽△BEC;
(2)一名同学在尝试了上题后还发现:如图②、图③,只要A,E,B三点在同一直线上,且∠A=∠B=∠DEC,则(1)中的结论总成立.你同意吗?请选择其中之一说明理由.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.

(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是由几个小立方块所搭几何体的俯视圈,小立方块中的数字表示在该位置小立方块的个数.
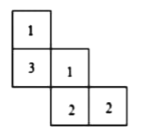
(1)请在网格内画出从正面和从左面看到的这个几何体的形状图.
(2)如图,是小明用9个棱长为1![]() 的小立方块积木搭成的几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数,他请小亮用尽可能少的同样大小的立方块在旁边再搭建一个几何体,使小亮所搭建的几何体恰好可以和小明所搭建的几何体拼成一个大的正方体(即拼大正方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
的小立方块积木搭成的几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数,他请小亮用尽可能少的同样大小的立方块在旁边再搭建一个几何体,使小亮所搭建的几何体恰好可以和小明所搭建的几何体拼成一个大的正方体(即拼大正方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
①小亮至少还需要 个小正方体;
②上面①中小亮所搭几何体的表面积为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
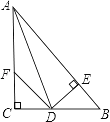
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强校园周边治安综合治理,警察巡逻车在学校旁边的一条东西方向的公路上执行治安巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程(单位:千米)为:![]()
(1)此时,这辆巡逻车司机如何向警务处描述他现在的位置?
(2)已知每千米耗油![]() 升,如果警务处命令其巡逻车马上返回出发点,这次巡逻共耗油多少升?
升,如果警务处命令其巡逻车马上返回出发点,这次巡逻共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
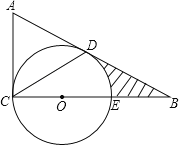
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com