
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.

(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
【答案】(1)AC=CD(2)OD=1
【解析】
解:(1)AC=CD,理由如下:
∵OA=OB,∴∠OAB=∠B。
∵直线AC为圆O的切线,∴∠OAC=∠OAB+∠DAC=90°。
∵OB⊥OC,∴∠BOC=90°。∴∠ODB+∠B=90°。
∵∠ODB=∠CDA,∴∠CDA+∠B=90°。
∴∠DAC=∠CDA。∴AC=CD。
(2)在Rt△OAC中,AC=CD=2,AO=![]() ,OC=OD+DC=OD+2,
,OC=OD+DC=OD+2,
根据勾股定理得:OC2=AC2+AO2,即(OD+2)2=22+(![]() )2,
)2,
解得:OD=1(负值已舍去)。
(1)AC=CD,理由为:由AC为圆的切线,利用切线的性质得到∠OAC为直角,再由OC与OB垂直,得到∠BOC为直角,由OA=OB,利用等边对等角得到一对角相等,再利用对顶角相等及等角的余角相等得到一对角相等,利用等角对等边即可得证。
(2)由ODC=OD+DC,DC=AC,表示出OC,在直角三角形OAC中,利用勾股定理即可求出OD的长。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-20,
点对应的数为-20,![]() 点对应的数为100.
点对应的数为100.

(1)请写出![]()
![]() 中点
中点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚊![]() 从
从![]() 点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁
点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(3)若当电子蚂蚁![]() 从
从![]() 点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一副三角板![]() 和
和![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
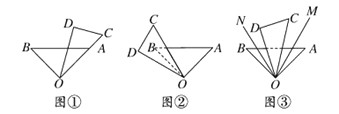
(1)如图①,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() 的度数是______________.
的度数是______________.
(2)如图②,变化摆放位置将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,若
逆时针方向转动,若![]() 恰好平分
恰好平分![]() ,则
,则![]() 的度数是__________;
的度数是__________;
(3)如图③,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .如果三角板
.如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
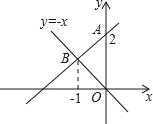
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为![]() 的中点,连接DE,EB.
的中点,连接DE,EB.
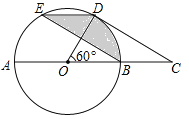
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
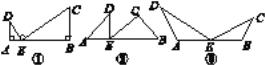
【题目】(1)尝试:如图①,已知A,E,B三点在同一直线上,且∠A=∠B=∠DEC=90°,求证:△ADE∽△BEC;
(2)一名同学在尝试了上题后还发现:如图②、图③,只要A,E,B三点在同一直线上,且∠A=∠B=∠DEC,则(1)中的结论总成立.你同意吗?请选择其中之一说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进![]() 步后退
步后退![]() 步的程序运动,设该机器人每秒钟前进或后退
步的程序运动,设该机器人每秒钟前进或后退![]() 步,并且每步的距离为
步,并且每步的距离为![]() 个单位长,
个单位长,![]() 表示第
表示第![]() 秒时机器人在数轴上的位置所对应的数,给出下列结论(1)
秒时机器人在数轴上的位置所对应的数,给出下列结论(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() 其中,正确结论的个数是( )
其中,正确结论的个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①![]() =
=![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+![]() .其中正确的是( )
.其中正确的是( )

A. ①③④ B. ①②③ C. ①② D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com