
【题目】如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①![]() =
=![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+![]() .其中正确的是( )
.其中正确的是( )

A. ①③④ B. ①②③ C. ①② D. ③④
【答案】C
【解析】①连接OA,OB,根据正方形的性质,知∠AOB=90°=∠EOF,又∠BOE共用,故可得∠AOE=∠BOF,再根据圆心角定理可得①![]() =
=![]() ;故①正确;
;故①正确;
②连接OB,OC,证明△OGB≌△OHC,可得OG=OH,即可得出△OGH是等腰直角三角形;故②正确;
③过点O作OM⊥BC,ON⊥AB,易证得△OGN≌△OHM,因此可得出S△OGN=S△OHM,故不管点E的位置如何变化,四边形OGBH的面积不变;故③错误;
④过点B作B关于OF的对称点P(易知点P在⊙O上),连接PH,则PH=BH;过点B作B关于OE的对称点Q(易知点Q在⊙O上),连接QG,则QG=BG;连接PQ,易证明PQ过圆心O,则PQ=![]() =4
=4![]() ≠4+
≠4+![]() ,故④错误.
,故④错误.
①如图所示,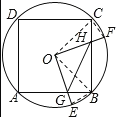
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,

∴△BOE≌△COF,
∴BE=CF,
∴![]() ,①正确;
,①正确;
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④过点B作B关于OF的对称点P(易知点P在⊙O上),连接PH,则PH=BH;过点B作B关于OE的对称点Q(易知点Q在⊙O上),连接QG,则QG=BG;
连接PQ,易证明PQ过圆心O,
∴PQ=![]() =4
=4![]() ≠4+
≠4+![]() ,
,
故④错误.
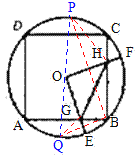
综上,①②正确,③④错误.
故选:C


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.

(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强校园周边治安综合治理,警察巡逻车在学校旁边的一条东西方向的公路上执行治安巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程(单位:千米)为:![]()
(1)此时,这辆巡逻车司机如何向警务处描述他现在的位置?
(2)已知每千米耗油![]() 升,如果警务处命令其巡逻车马上返回出发点,这次巡逻共耗油多少升?
升,如果警务处命令其巡逻车马上返回出发点,这次巡逻共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
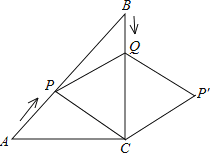
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
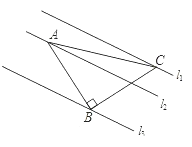
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1、l2之间的距离为2,l2、l3之间的距离为3,则AC的长是_________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.

(1)求证:CA2=CE CD;
(2)已知CA=5,EC=3,求sin∠EAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
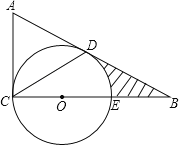
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
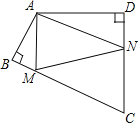
A. 130°B. 120°C. 110°D. 100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com