
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
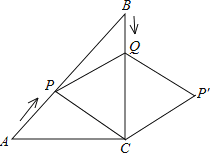
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进![]() 步后退
步后退![]() 步的程序运动,设该机器人每秒钟前进或后退
步的程序运动,设该机器人每秒钟前进或后退![]() 步,并且每步的距离为
步,并且每步的距离为![]() 个单位长,
个单位长,![]() 表示第
表示第![]() 秒时机器人在数轴上的位置所对应的数,给出下列结论(1)
秒时机器人在数轴上的位置所对应的数,给出下列结论(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() 其中,正确结论的个数是( )
其中,正确结论的个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①![]() =
=![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+![]() .其中正确的是( )
.其中正确的是( )

A. ①③④ B. ①②③ C. ①② D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com