
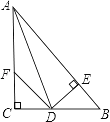
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用HL证明RT△CDF≌RT△EDB即可得出CF=EB;
(2)利用HL证明RT△ADE≌RT△ADC即可得出AC=AE,再由AB=AE+EB=AF+CF+EB进行等量代换即可.
(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL)
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.


科目:初中数学 来源: 题型:
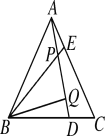
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 互为相反数,
互为相反数,![]() 互为倒数,且
互为倒数,且![]() 的立方等于它本身.
的立方等于它本身.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 试讨论:当
试讨论:当![]() 为有理数时,
为有理数时,![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
![]() 若
若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出![]() =83分,
=83分,![]() =82分,绘制成如下尚不完整的统计图表.
=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
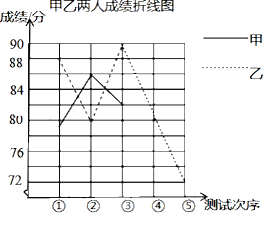
(1)a=
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
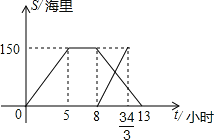
【题目】黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并。立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇对,两船与黄岩岛的距离、
(3在渔政船驶往黄岩岛的过程中,求渔船从港口 出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:折纸中的数学
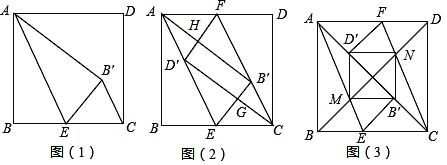
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,分别指出两个图形中的等腰三角形,并利用第一个图证明结论。
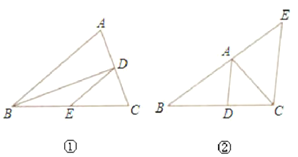
(1)如图①,BD平分∠ABC,DE//AB
(2) 如图②,AD平分∠BAC , EC//AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com