
【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

【答案】(1)证明见解析;(2)四边形DEGF是菱形.理由见解析.
【解析】试题分析:(1)根据正方形的性质可得AD=CD,∠A=∠C=90°,然后利用“角边角”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CF;
(2)求出BE=BF,再求出DE=DF,再根据到线段两端点距离相等的点在线段的垂直平分线可得BD垂直平分EF,然后根据对角线互相垂直平分的四边形是菱形证明.
试题解析:(1)证明:在正方形ABCD中,AD=CD,∠A=∠C=90°,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF;
(2)四边形DEGF是菱形.
理由如下:在正方形ABCD中,AB=BC,
∵AE=CF,
∴AB﹣AE=BC﹣CF,
即BE=BF,
∵△ADE≌△CDF,
∴DE=DF,
∴BD垂直平分EF,
又∵OG=OD,
∴四边形DEGF是菱形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在学校举办的“中华诗词大赛”中,有11名选手进入决赛,他们的决赛成绩各不相同,其中一名参赛选手想知道自己是否能进入前6名,他需要了解这11名学生成绩的( )
A.中位数
B.平均数
C.众数
D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在平面直角坐标系xOy中,抛物线![]() 过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.

(1)求b、c的值;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
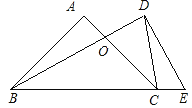
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x-3)(x2-4x+1)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y-3)(y+1)+4 (第一步)
= y2-2y+1 (第二步)
=(y-1)2 (第三步)
=(x2-4x-1)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为( )
A.2.01×10﹣6千克
B.0.201×10﹣5千克
C.20.1×10﹣7千克
D.2.01×10﹣7千克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com