
����Ŀ��ij��ҵΪ���ݼ������ҵ�����ṩ�������������Ԫ�ߵ͵�Ӱ�죬��ȥ��1��9�£��������ԭ���ϼ۸�һ·������ÿ�������ԭ���ϼ۸�y1��Ԫ�����·�x��1��x��9����xȡ������֮��ĺ�����ϵ���±���
�·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
�۸�y1��Ԫ/���� | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
���Ź��ҵ��ش�ʩ�ij�̨��ԭ���ϼ۸������������10��12��ÿ�������ԭ���ϼ۸�y2��Ԫ�����·�x��10��x��12����xȡ������֮�������ͼ��ʾ�ı仯���ƣ�
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶ��ֱ��д��y1 ��x֮��ĺ�����ϵʽ��������ͼ��ʾ�ı仯���ƣ�ֱ��д��y2��x֮�������һ�κ�����ϵʽ��
��2����ȥ������ÿ�����ۼ�Ϊ1000Ԫ������ÿ������������ɱ�Ϊ50Ԫ�������ɱ�30Ԫ���������1��9�µ�������p1����������·�x�����ϵʽp1=0.1x+1.1��1��x��9����xȡ��������10��12�µ�������p2�������p2=��0.1x+2.9��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������

���𰸡���1��y1=20x+540��y2=10x+630����2��ȥ��4�����۸��������������������Ϊ450��Ԫ��
��������
��1�����ô���ϵ���������ͼ���ϵ���������һ�κ�������ʽ���ɣ�
��2����������ÿ������������ɱ�Ϊ50Ԫ�������ɱ�30Ԫ���Լ��ۼ�������������������
��1�����ñ���ó�������ϵ��һ�κ�����ϵ��
��y1=kx+b��
��![]()
��ã�![]()
��y1=20x+540��
����ͼ��ó�������ϵ��һ�κ�����ϵ��
��y2=ax+c��
��![]()
��ã� ![]()
��y2=10x+630��
��2��ȥ��1��9��ʱ�����۸����������w=p1��1000��50��30��y1����
=��0.1x+1.1����1000��50��30��20x��540��=��2x2+16x+418��
=��2�� x��4��2+450����1��x��9����xȡ������
����2��0��1��x��9���൱x=4ʱ��w���=450����Ԫ����
ȥ��10��12��ʱ�����۸����������w=p2��1000��50��30��y2��
=����0.1x+2.9����1000��50��30��10x��630����
=�� x��29��2����10��x��12����xȡ��������
��10��x��12ʱ���൱x=10ʱ��w���=361����Ԫ����
��450��361����ȥ��4�����۸��������������������Ϊ450��Ԫ��


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ����B����
����B����![]() �ĶԳƵ�Eǡ������
�ĶԳƵ�Eǡ������![]() �ϣ���
�ϣ���![]() ����
����![]() �Ķ���Ϊ������������
�Ķ���Ϊ������������

A.45��B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵ����ߣ���֤��AD��BC.
�����)

֤������AD��BC���ϵ�����
��BD=CD(���ߵ�����)
�ڡ�ABD�͡�ACD��
�� 
��________����________����________.
�� ________�� ________��________��
���ADB=________��________��
���ADB= ![]() ��BDC=90��(ƽ�ǵĶ���)
��BDC=90��(ƽ�ǵĶ���)
��AD��BC����ֱ�Ķ��壩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴����л����㴫ͳ�Ļ����н����־�����չ�������ж���У�����ijУ��ί��֯���꼶100��ѧ�������������ж���ѡ�����������ȫ�����ѧ���ijɼ������������õ����в�������ͳ��ͼ����
��� | ������ | Ƶ�� | Ƶ�� |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
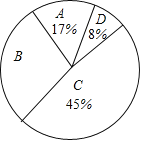
�����������Ϣ������������⣺
(1)����a=___��b=___��
(2)���������ͳ��ͼ��B���Ӧ���ε�Բ�ĽǵĶ�����
(3)��֪������ͬѧ��ȡ��98�ֵ���óɼ������а�������ͬһ�༶�ļס�������ͬѧ��ѧУ����������ͬѧ�����ѡ�������μ��м������������б�������״ͼ����ס�������ͬѧ����ѡ�еĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ƽ���˾����A,B���ֶ�ý�壬�����ֶ�ý��Ľ������ۼ������ʾ��

�ý����Ƽ���˾�ƻ��������ֶ�ý�干50�ף������ʽ�132��Ԫ .
(1)�ý����Ƽ���˾�ƻ�����A,B���ֶ�ý��������ף�
(2)�����г�������̵������ԭ�ƻ�50��ý��Ļ����ϣ�����A�Ĺ�������������B �Ĺ�����������֪B�ֶ�ý�����ӵ�������A�ֶ�ý�����������1.5����ȫ�����ۺ���Ի�ȡë����21��Ԫ����ʵ�ʹ���A�ֶ�ý������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��AB=AC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E����F��AC���ӳ����ϣ��ҡ�CBF=![]() ��CAB��
��CAB��
��1����֤��ֱ��BF�ǡ�O�����ߣ�
��2����AB=5��sin��CBF=![]() ,��BC��BF�ij���
,��BC��BF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC.
��1���߹���ͼ������C��AB�Ĵ��߽�AB�ڵ�O.��д������������ͼ�ۼ���
��2���ֱ���ֱ��AB��OCΪx�ᣬy�Ὠ��ƽ��ֱ������ϵ��ʹ��B��C ������������.��AB=7.5��OC=4.5����A=45����д����B����y��ĶԳƵ�D�����ꣻ
��3���ڣ�2���������£�����ACD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ֱ��������OAA1��ֱ�DZ�OA��x���ϣ���A1�ڵ�һ���ޣ���OA��1���Ե�A1Ϊֱ�Ƕ��㣬0A1Ϊһֱ�DZ�������ֱ��������OA1A2�����Ե�A2Ϊֱ�Ƕ��㣬OA2Ϊֱ�DZ�������ֱ��������OA2A3�����˹��ɣ����A2019��������_____��
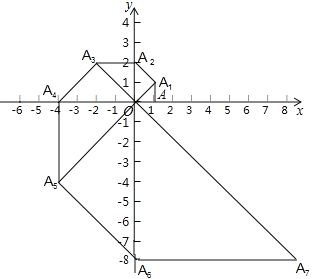
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com