
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
【答案】(1)政府这个月为他承担的总差价为600元.(2)当销售单价定为30元时,每月可获得最大利润4000元.(3)销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
【解析】
试题分析:(1)把x=20代入y=﹣10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由总利润=销售量每件纯赚利润,得w=(x﹣10)(﹣10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令﹣10x2+600x﹣5000=3000,求出x的值,结合图象求出利润的范围,然后设政府每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
解:(1)当x=20时,y=﹣10x+500=﹣10×20+500=300,
300×(12﹣10)=300×2=600元,
即政府这个月为他承担的总差价为600元.
(2)由题意得,w=(x﹣10)(﹣10x+500)
=﹣10x2+600x﹣5000
=﹣10(x﹣30)2+4000
∵a=﹣10<0,∴当x=30时,w有最大值4000元.
即当销售单价定为30元时,每月可获得最大利润4000元.
(3)由题意得:﹣10x2+600x﹣5000=3000,
解得:x1=20,x2=40.
∵a=﹣10<0,抛物线开口向下,
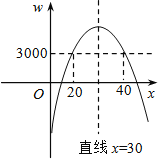
∴结合图象可知:当20≤x≤40时,4000>w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12﹣10)×(﹣10x+500)
=﹣20x+1000.
∵k=﹣20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图1,二次函数y=ax2﹣2ax+c(a>0)的图象与y轴交于点C(0,﹣4),与x轴交于点A、B两点,点A的坐标为(4,0).

(1)求该抛物线的函数解析式;
(2)点P(t,0)是线段OB上一动点(不与O、B重合),点E是线段BC上的点,以点B、P、E为顶点的三角形与三角形ABC相似,连结CP,求△CPE的面积S与t的函数关系式;
(3)如图2,若平行于x轴的动直线与该抛物线交于点Q,与直线AC交于点F,点D的坐标为(2,0),则存在这样的直线,使得△ODF为等腰三角形,请直接写出点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
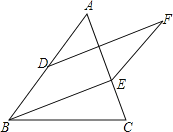
(1)猜想:DF与AE的关系是 ;
(2)试说明你猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com