练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
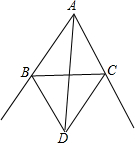
    3．如图，已知，△ABC的∠B，∠C的外角平分线交于点D，AD是∠BAC的平分线吗？说明理由．

    分析 首先作辅助线：分别过D作DE、DF、DG垂直于AB、BC、AC，垂足分别为E、F、G，然后利用角的平分线上的点到角的两边的距离相等可知DE=DG，再利用到角两边距离相等的点在角的平分线上的逆定理证明．

    解答 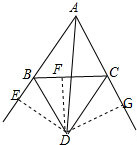证明：分别过D作DE、DF、DG垂直于AB、BC、AC，垂足分别为E、F、G，作射线AD，
    ∵BD平分∠CBE，DE⊥BE，DF⊥BC，
    ∴DE=DF，
    同理DG=DF，
    ∴DE=DG，
    ∴点D在∠EAG平分线上，
    ∴AD是∠BAC的平分线．

    点评 本题考查了角平分线的性质及其逆用；解题的关键是作辅助线，辅助线是证明一道题的重中之重，然后利用到角两边距离相等的点在角的平分线上的逆定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．如图，线段AB与CD相交于点O，OA=OC，还需增加一个条件，OD=OB，使得△AOD≌△COB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

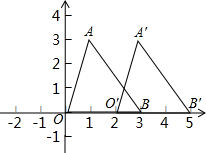    14．如图，三角形AOB的顶点A，B的坐标分别为（1，3），（3，0），经过平移，三角形AOB变成了三角形A′O′B′，其中点O′的坐标为（2，0），试写出点A′，B′的坐标，平面上任一点P（x，y）在这个平移下的像为点P′（x′，y′），试问：点P′的坐标与点P的坐标之间有什么关系呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，AD⊥BC于D，F在AD上，且CF=AB，若DF=BD，求证：CF⊥AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．用代入法解下列方程组．
    （1）$\left\{\begin{array}{l}{3x+4y=16}\\{5x-6y=33}\end{array}\right.$．
    （2）$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{4（x+y）-5（x-y）=2}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．求∠A+∠B+∠C+∠D+∠E+∠F为多少度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程：$\frac{1}{2}$x+30+x=180．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

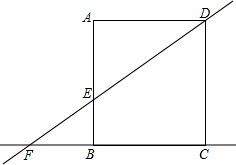    3．如图，在矩形ABCD中，AD=8，直线DE交直线AB于点E，交直线BC于F，AE=6．
    （1）若点P是边AD上的一个动点（不与点A、D重合），PH⊥DE于H，设DP为x，四边形AEHP的面积为y，试求y与x的函数解析式；
    （2）若AE=2EB．
    ①求圆心在直线BC上，且与直线DE、AB都相切的⊙O的半径长；
    ②圆心在直线BC上，且与直线DE及矩形ABCD的某一边所在直线都相切的圆共有多少个？（直接写出满足条件的圆的个数即可．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解不等式组$\left\{\begin{array}{l}\frac{2x-1}{3}-\frac{5x+1}{2}≤2\\ 5x-1＜3（x+1）\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案