
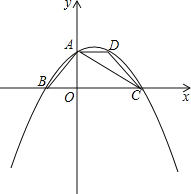
【题目】如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2![]() ,连接AC.
,连接AC.

(1)求出直线AC的函数解析式;
(2)求过点A,C,D的抛物线的函数解析式;
(3)在抛物线上有一点P(m,n)(n<0),过点P作PM垂直于x轴,垂足为M,连接PC,使以点C,P,M为顶点的三角形与Rt△AOC相似,求出点P的坐标.
【答案】(1)y=﹣![]() x+2;(2)y=﹣
x+2;(2)y=﹣![]() x2+
x2+![]() x+2;(3)点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).
x+2;(3)点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).
【解析】
试题分析:(1)先在Rt△ABO中,运用勾股定理求出OB=![]() =
=![]() =2,得出B(﹣2,0),再根据等腰梯形的对称性可得C点坐标为(4,0),又A(0,2),利用待定系数法即可求出直线AC的函数解析式;
=2,得出B(﹣2,0),再根据等腰梯形的对称性可得C点坐标为(4,0),又A(0,2),利用待定系数法即可求出直线AC的函数解析式;
(2)设所求抛物线的解析式为y=ax2+bx+c,将A,C,D三点的坐标代入,利用待定系数法即可求出抛物线的函数解析式;
(3)先由点P(m,n)(n<0)在抛物线y=﹣![]() x2+
x2+![]() x+2上,得出m<﹣2或m>4,n=﹣
x+2上,得出m<﹣2或m>4,n=﹣![]() m2+
m2+![]() m+2<0,于是PM=
m+2<0,于是PM=![]() m2﹣
m2﹣![]() m﹣2.由于∠PMC=∠AOC=90°,所以当Rt△PCM与Rt△AOC相似时,有
m﹣2.由于∠PMC=∠AOC=90°,所以当Rt△PCM与Rt△AOC相似时,有![]() =
=![]() =
=![]() 或
或![]() =
=![]() =2.再分两种情况进行讨论:①若m<﹣2,则MC=4﹣m.由
=2.再分两种情况进行讨论:①若m<﹣2,则MC=4﹣m.由![]() =
=![]() =
=![]() ,列出方程
,列出方程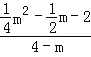 =
=![]() ,解方程求出m的值,得到点P的坐标为(﹣4,﹣4);由
,解方程求出m的值,得到点P的坐标为(﹣4,﹣4);由![]() =
=![]() =2,列出方程
=2,列出方程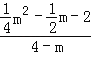 =2,解方程求出m的值,得到点P的坐标为(﹣10,﹣28);②若m>4,则MC=m﹣4.由
=2,解方程求出m的值,得到点P的坐标为(﹣10,﹣28);②若m>4,则MC=m﹣4.由![]() =
=![]() =
=![]() 时,列出方程
时,列出方程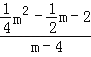 =
=![]() ,解方程求出m的值均不合题意舍去;由
,解方程求出m的值均不合题意舍去;由![]() =
=![]() =2,列出方程
=2,列出方程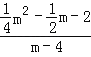 =2,解方程求出m的值,得到点P的坐标为(6,﹣4).
=2,解方程求出m的值,得到点P的坐标为(6,﹣4).
解:(1)由A(0,2)知OA=2,
在Rt△ABO中,∵∠AOB=90°,AB=2![]() ,
,
∴OB=![]() =
=![]() =2,
=2,
∴B(﹣2,0).
根据等腰梯形的对称性可得C点坐标为(4,0).
设直线AC的函数解析式为y=kx+n,
则![]() ,解得
,解得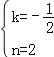 ,
,
∴直线AC的函数解析式为y=﹣![]() x+2;
x+2;
(2)设过点A,C,D的抛物线的函数解析式为y=ax2+bx+c,
则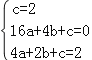 ,解得
,解得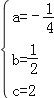 ,
,
∴y=﹣![]() x2+
x2+![]() x+2;
x+2;
(3)∵点P(m,n)(n<0)在抛物线y=﹣![]() x2+
x2+![]() x+2上,
x+2上,
∴m<﹣2或m>4,n=﹣![]() m2+
m2+![]() m+2<0,
m+2<0,
∴PM=![]() m2﹣
m2﹣![]() m﹣2.
m﹣2.
∵Rt△PCM与Rt△AOC相似,
∴![]() =
=![]() =
=![]() 或
或![]() =
=![]() =2.
=2.
①若m<﹣2,则MC=4﹣m.
当![]() =
=![]() =
=![]() 时,
时,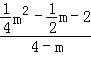 =
=![]() ,
,
解得m1=﹣4,m2=4(不合题意舍去),
此时点P的坐标为(﹣4,﹣4);
当![]() =
=![]() =2时,
=2时,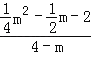 =2,
=2,
解得m1=﹣10,m2=4(不合题意舍去),
此时点P的坐标为(﹣10,﹣28);
②若m>4,则MC=m﹣4.
当![]() =
=![]() =
=![]() 时,
时,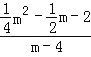 =
=![]() ,
,
解得m1=4,m2=0,均不合题意舍去;
当![]() =
=![]() =2时,
=2时,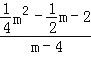 =2,
=2,
解得m1=6,m2=4(不合题意舍去),
此时点P的坐标为(6,﹣4);
综上所述,所求点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).


科目:初中数学 来源: 题型:
【题目】将多项式ax2-4ax+4a分解因式,下列结果中正确( )
A. a(x-2)2 B. a(x+2)2
C. a(x-4)2 D. a(x+2)(x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级二班在订购本班的班服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150160cm以下记为M号,160170cm以下记为L号.170cm 以上记为XL号.若用统计图描述这些数据,合适的统计图是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
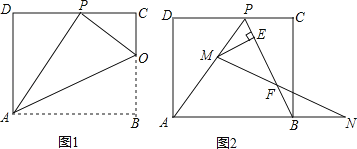
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,![]()
![]()
![]()
![]()
![]()
![]() ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年山东省高考报名人数位居全国第三,约有696000人报名,将696000用科学记数法表示为( )
A.69.6×104
B.6.96×105
C.6.96×106
D.0.696×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
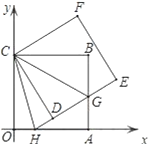
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com