
【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP= ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:∵AB是⊙O的直径,
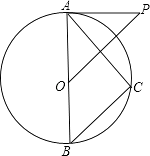
∴∠ACB=90°,
∴∠BAC+∠B=90°.
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°.
∵∠P=∠BAC.
∴∠P+∠AOP=90°,
∴由三角形内角和定理知∠PAO=90°,即OA⊥AP.
又∵OA是的⊙O的半径,
∴PA为⊙O的切线
(2)解:由(1)知,∠PAO=90°.∵OB=5,
∴OA=OB=5.
又∵OP= ![]() ,
,
∴在直角△APO中,根据勾股定理知PA= ![]() =
= ![]() ,
,
由(1)知,∠ACB=∠PAO=90°.
∵∠BAC=∠P,
∴△ABC∽△POA,
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ,
,
解得AC=8.即AC的长度为8.
【解析】(1)欲证明PA为⊙O的切线,只需证明OA⊥AP;(2)通过相似三角形△ABC∽△PAO的对应边成比例来求线段AC的长度.
【考点精析】本题主要考查了勾股定理的概念和切线的判定定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.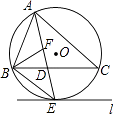
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为米. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A3的坐标是 , A92的坐标是 . 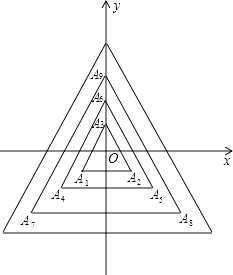
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象. 
(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )
A.x1<x2<a<b
B.x1<a<x2<b
C.x1<a<b<x2
D.a<x1<b<x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )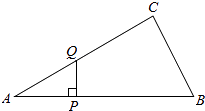
A.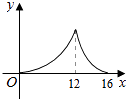
B.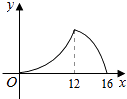
C.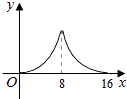
D.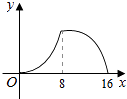
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE. 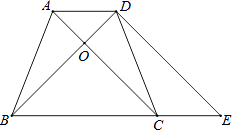
(1)求证:BD=DE.
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 .
在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com