
【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售![]() 元,在果园每千克售
元,在果园每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用![]() 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
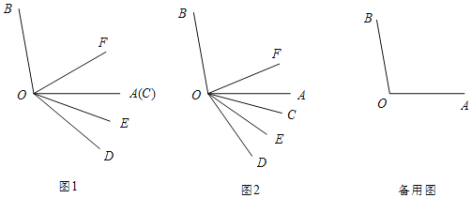
【题目】已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.
(1)如图1,当OA,OC重合时,求∠EOF的度数;
(2)若将∠COD的从图1的位置绕点O顺时针旋转,旋转角∠AOC=α,且0°<α<90°.
①如图2,试判断∠BOF与∠COE之间满足的数量关系并说明理由.
②在∠COD旋转过程中,请直接写出∠BOE,∠COF,∠AOC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑、白正方形按如图规律排列.

(1)第10个和第11图形中,黑色正方形各有多少个?
(2)找出图形变化的规律,说明第n个图形中黑色正方形的个数与n的关系.
(3)这列图形中,是否存在黑色正方形的个数为2019的图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017贵州省遵义市)如图,抛物线![]() (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为![]() .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
②试求出此旋转过程中,(NA+![]() NB)的最小值.
NB)的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
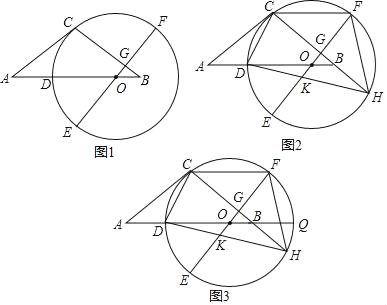
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com