
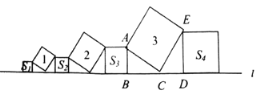
【题目】在直线![]() 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是
上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是![]() ,则
,则![]() _______.
_______.
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递员开摩托车从总部A点出发,在一条南北公路上来回收取包裹,现在记录下他连续行驶的情况(以向南为正方向,单位:千米):5,2,-4,![]() ,3,-2.5,6.请问
,3,-2.5,6.请问
(1)他最后一次收取包裹后在出发点A的什么位置?
(2)如果摩托车每千米耗油30毫升,出发前摩托车有油1000毫升,快递员在收完包裹后能回到总部吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2
B、4
C、![]()
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少
或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少![]() (步距是指每一步的距离),两人各跑了
(步距是指每一步的距离),两人各跑了![]() 圈,跑
圈,跑![]() 圈前后的时刻和步数如下:
圈前后的时刻和步数如下:
出发时刻 | 出发时微信运动中显示的步数 | 结束时刻 | 结束时微信运动中显示的步数 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)求甲、乙的步距和环形道的周长;
(2)若每![]() 分钟甲比乙多跑
分钟甲比乙多跑![]() 步,求表中
步,求表中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察数轴,请回答:
![]()
(1)点![]() 与点
与点![]() 的距离为 ,点
的距离为 ,点![]() 与点
与点![]() 的距离为 ;
的距离为 ;
点![]() 与点
与点![]() 的距离为 ,点
的距离为 ,点![]() 与点
与点![]() 的距离为 ;
的距离为 ;
(2)发现:在数轴上,如果点![]() 与点
与点![]() 分别表示数
分别表示数![]() ,则它们之间的距离可表示为
,则它们之间的距离可表示为![]() (用
(用![]() 表示);
表示);
(3)利用发现的结论,逆向思维解决下列问题:
①数轴上表示![]() 的点
的点![]() 与
与![]() 之间的距离是
之间的距离是![]() ,则
,则![]() 的值是 ;
的值是 ;
②![]() ,则
,则![]() ;
;
③数轴上是否存在表示![]() 的点
的点![]() ,使点
,使点![]() 到点
到点![]() 、点
、点![]() 的距离之和为
的距离之和为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
④![]() 的最小值为 ;
的最小值为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售![]() 元,在果园每千克售
元,在果园每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用![]() 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com