
【题目】已知二次函数y=﹣2x2﹣4x+6.
(1)求出函数的顶点坐标、对称轴以及描述该函数的增减性.
(2)求抛物线与x轴交点和y轴交点坐标;并画出它的大致图象.
(3)当﹣2<x<4时.求函数y的取值范围.
【答案】(1)顶点坐标(﹣1,8),对称轴x=﹣1,当x≤﹣1时,y随着x的增大而增大,当x≥﹣1时,y随着x的增大而减小;(2)函数图象与x轴交点坐标(1,0),(﹣3,0),与y轴交点坐标(0,6),图象见解析;(3)﹣42<y≤8.
【解析】
(1)顶点坐标为(﹣![]() )对称轴是x=﹣
)对称轴是x=﹣![]() ,据对称轴的左侧还是右侧来进行判断函数值随自变量的变化;
,据对称轴的左侧还是右侧来进行判断函数值随自变量的变化;
(2)与x轴的坐标y=0,与y轴的交点坐标x=0;
(3)根据图象即可得到结论.
(1)∵a=﹣2,b=﹣4,c=6,∴﹣![]() =﹣
=﹣![]() =﹣1,
=﹣1,![]() =
=![]() =8,∴顶点坐标(﹣1,8),对称轴x=﹣1.当x≤﹣1时,y随着x的增大而增大,当x≥﹣1时,y随着x的增大而减小;
=8,∴顶点坐标(﹣1,8),对称轴x=﹣1.当x≤﹣1时,y随着x的增大而增大,当x≥﹣1时,y随着x的增大而减小;
(2)当y=0时,﹣2x2﹣4x+6=0,∴x1=﹣3,x2=1,当x=0时,y=6,∴函数图象与x轴交点坐标(1,0),(﹣3,0),与y轴交点坐标(0,6);
(3)由图象可知:
当﹣2<x<4时,函数y的取值范围﹣42<y≤8.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)是由抛物线y=﹣x2+x+2先作关于y轴的轴对称图形,再将所得到的图象向下平移3个单位长度得到的,点Q1(﹣2.25,q1),Q2(1.5,q2)都在抛物线y=ax2+bx+c(a≠0)上,则q1,q2的大小关系是( )
A. q1>q2 B. q1<q2 C. q1=q2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
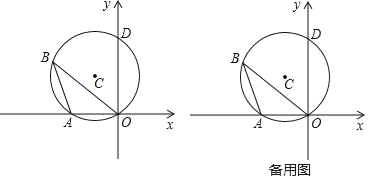
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月份,我县教体局由县城老区搬到了新区(海丰16路与棣新4路交叉口),当时某科室需要把相关档案由老区办公楼搬到新区办公楼,甲搬家公司单独工作了3天,完成总量的![]() ;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD,交OD的延长线于点A,连接BC,∠B=∠A=30,BD=![]() 。
。
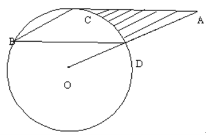
(1)求证:AC是⊙O的切线。
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积(结果保留π)。
查看答案和解析>>
科目:初中数学 来源: 题型:
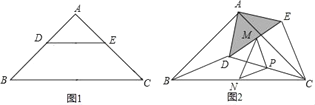
【题目】如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,
(1)求证:∠B=∠C,AD=AE;
(2)若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
①判断△PMN的形状,并说明理由;
②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com