
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
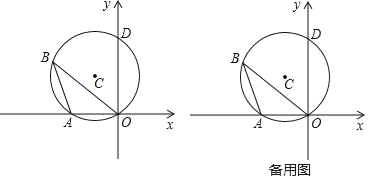
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
【答案】(1)(﹣1, ![]() );(2)B(﹣3,
);(2)B(﹣3, ![]() );(3)B(﹣
);(3)B(﹣![]() ﹣1,
﹣1, ![]() +1)或B(
+1)或B(![]() ﹣1,
﹣1, ![]() ﹣1).
﹣1).
【解析】试题分析:(1)连接OC并延长,交⊙C于点E,连接EA、ED,在直角三角形中,由30°角的性质和直角三角形的正切值可求出ED的长;再过点C作CF⊥OD,垂足为F,则CF是△DEO的中位线,根据三角形的中位线的性质可求C点的坐标;
(2)作BH⊥x轴交x轴于点H,根据勾股定理可求B点的坐标;
(3)分为B点在第一象限或第二象限,设出B的坐标,利用勾股定理可求解.
试题解析:(1)如图1,连接OC并延长,交⊙C于点E,连接EA、ED.
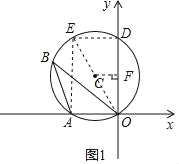
因为∠ABO=30°,
∴∠AEO=30°,又因为OE是直径,
∠AOE=60°,∠EOD=30°,∠EDO=90°
∵OD=2![]() ,
,
∴ED=DOtan30°=2.
过点C作CF⊥OD,垂足为F,则CF是△DEO的中位线,
所以OF=![]() ,CF=1.
,CF=1.
∴点C的坐标为(﹣1,![]() )
)
故圆心C的坐标为(﹣1,![]() );
);
(2)如图2,作BH⊥x轴交x轴于点H,
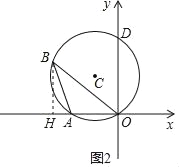
当△BOD是等边三角形,
则OB=OD=2![]() ,∠BOD=60°,
,∠BOD=60°,
故∠BOA=30°,
则BH=![]() OB=
OB=![]() ×2
×2![]() =
=![]() ,
,
OH=![]() =
=![]() =3,
=3,
∴B(﹣3,![]() );
);
(3
则BC=![]() ,
,
∴AD=![]() =
=![]() =4,
=4,
∴AC=2,
∵BC=AC,
∴![]() =2,
=2,
∴(﹣a+1)2+(a﹣![]() )2=4,
)2=4,
解得:a1=0(舍去),a2=1+![]() ,
,
故B(﹣![]() ﹣1,
﹣1,![]() +1),
+1),
若B在第一象限,设B(a,a),(a>0),
∴BC=![]() ,
,
同理:![]() =2,
=2,
解得:a3=0(舍去),a4=![]() ﹣1,
﹣1,
∴B(![]() ﹣1,
﹣1,![]() ﹣1),
﹣1),
综上所述:B(﹣![]() ﹣1,
﹣1,![]() +1)或B(
+1)或B(![]() ﹣1,
﹣1,![]() ﹣1).
﹣1).


科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车的熬油情况,将油箱加满后进行了耗油实验,得到如下数据:
轿车行驶的路程 |
|
|
|
|
| ··· |
油箱剩余油量 |
|
|
|
|
| ··· |
(1)该轿车油箱的容量为 ![]() ,行驶
,行驶![]() 时,油箱剩余油量为
时,油箱剩余油量为 ![]()
(2)根据上表的数据,写出油箱剩余油量![]() 与轿车行驶的路程
与轿车行驶的路程![]() 之间的表达式
之间的表达式![]() .
.
(3)某人将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱剩余油量为
地时油箱剩余油量为![]() ,求
,求![]() 两地之间的距离?
两地之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,则多了3钱,每人出7钱,则少4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C,D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
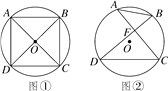
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在下面平面直角坐标系中,已知A ![]() ,B
,B ![]() ,C
,C ![]() 三点.其中
三点.其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]()
![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积为△
的面积为△![]() 的面积的两倍?若存在,求出点
的面积的两倍?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
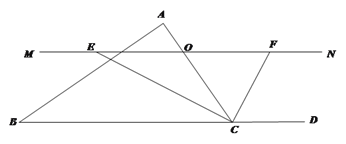
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com