
【题目】已知A,B,C,D是⊙O上的四个点.
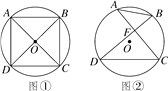
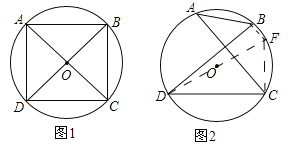
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O的半径为![]() .
.
【解析】试题分析:(1)根据题意不难证明四边形ABCD是正方形,结论可以得到证明;
(2)连结DO,延长交圆O于F,连结CF、BF.根据直径所对的圆周角是直角,得∠DCF=∠DBF=90°,则BF∥AC,根据平行弦所夹的弧相等,得弧CF=弧AB,则CF=AB.根据勾股定理即可求解.
试题解析:
:(1)∵∠ADC=∠BCD=90°,
∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,
∴四边形ABCD是矩形,
∵AD=CD,
∴四边形ABCD是正方形,
∴AC⊥BD;
(2)连结DO,延长交圆O于F,连结CF、BF.
∵DF是直径,
∴∠DCF=∠DBF=90°,
∴FB⊥DB,
又∵AC⊥BD,
∴BF∥AC,∠BDC+∠ACD=90°,
∵∠FCA+∠ACD=90°
∴∠BDC=∠FCA=∠BAC
∴等腰梯形ACFB
∴CF=AB.
根据勾股定理,得
CF2+DC2=AB2+DC2=DF2=20,
∴DF=2![]() ,
,
∴OD=![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
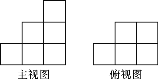
【题目】由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图29-29所示.
(1)请你画出这个几何体的一种左视图.
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
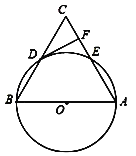
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
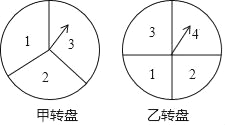
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
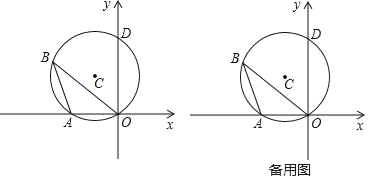
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,点A、D在l1上,AB⊥l1,CD⊥l2,垂足分别是B、C,点E,F在l2上,AE∥DF,那么AE与DF、BE与CF相等吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
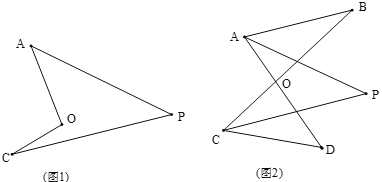
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
解决问题:
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
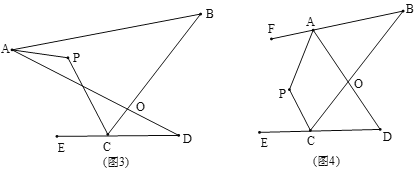
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com