【题目】如图，菱形ABCD中，AE⊥BC于点E，∠BAE=30°，AD=4cm．
（1）求菱形ABCD的各角的度数；
（2）求AE的长．
【答案】⑴菱形各角的度数为60°、120°、60°、120°；⑵AE的长为
cm
【解析】
（1）由AE⊥BC，得∠AEB＝90°,根据三角形的内角和即可求出∠B＝60°，
根据菱形的对角相等，邻角互补即可求解.
（2）根据菱形的四条边相等得到AB＝AD＝4，因为∠BAE＝30°，所以BE=2cm，利用勾股定理即可求出AE的长．
⑴ ∵AE⊥BC
∴∠AEB＝90°
∵∠BAE＝30°
∴∠B＝60°
∵菱形ABCD
∴∠D＝∠B＝60°，AB∥CD
∴∠BAD＝∠C＝120°
答：菱形各角的度数为60°、120°、60°、120°
⑵ ∵菱形ABCD
∴AB＝AD＝4
∵∠BAE＝30°
∴BE＝2
∴AE＝
答：AE的长为cm
数学奥赛暑假天天练南京大学出版社系列答案科目：初中数学 来源： 题型：
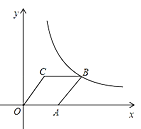
【题目】如图，菱形OABC的顶点C的坐标为（6，8）．顶点A在x轴的正半轴上，反比例函数
的图象经过顶B点.
（1）求点A和B的坐标；
（2）求k值及直线AB对应的函数解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了了解七年级
名学生其中数学考试情况，从中抽取了
名学生的数学成绩进行了统计，下面
个判断中正确的有（ ）个.
①这种调查的方式是抽样调查；②名学生是总体；③每名学生的数学成绩是个体；④名学生是总体的一个样本；⑤样本容量是.
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．
（1）求证：四边形BCED是平行四边形；
（2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某市城区地图(比例尺1∶9000)上，新安大街的图上长度与光华大街的图上长度分别是16 cm，10 cm.
(1)新安大街与光华大街的实际长度各是多少米？
(2)新安大街与光华大街的图上长度之比是多少？它们的实际长度之比呢？你发现了什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设边长为
的正方形的中心
在直线
上，它的一组对边垂直于直线，半径为
的圆的圆心
在直线上运动，、两点之间的距离为
．
（
）如图①，当
时，填表：
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
（
）如图②，⊙与正方形有
个公共点
、
、
、
、
，求此时与
之间的数量关系：
（
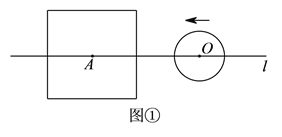
）由（）可知，、、之间的数量关系和⊙与正方形的公共点个数密切相关．当
时，请根据、、
之间的数量关系，判断⊙与正方形的公共点个数．
（
）当与之间满足（）中的数量关系时，⊙与正方形的公共点个数为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A(a,3)，点C(5，c)，点B的纵坐标为6且横纵坐标互为相反数，直线AC
轴，直线CB
轴：
(1)写出A、B、C三点坐标；
(2)求△ABC的面积；
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数，当△BCP的面积大于12小于16时，求点P横坐标取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
，点B在直线MN上，点A为直线PQ上一动点，连接AB.在直线AB的上方做
，使
，设
，
的平分线所在直线交PQ于点D．
（1）如图1，若
，且点C恰好落在直线MN上，则
________；
（2）如图2，若，且点C在直线MN右侧，求
的度数；
（3）若点C在直线MN的左侧，求的度数.（用含有α的式子表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1，可以得到
这个等式，请解答下列问题：
（1）写出图2中所表示的数学等式______________；（最后结果）
（2）根据整式乘法的运算法则，通过计算验证上述等式；
（3）利用（1）中得到的结论，解决问题：若a+b+c=10，ab+ac+bc=35，求a2+b2+c2的值；
（4）小明同学用图3中x张边长为a的正方形，y张边长为b的正方形，z张边长分别为a、b的长方形纸片拼出一个面积为（5a+2b）（3a+5b）的长方形，求x+y+z的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
