
【题目】提出问题:
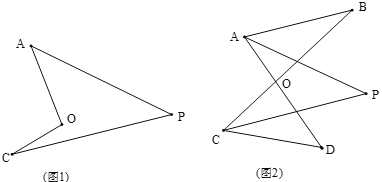
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
解决问题:
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
【答案】(1)∠AOC=∠A+∠P+∠C;(2)38°;(3)∠P=90°+![]() (∠B+∠D);(4)∠P=180°-
(∠B+∠D);(4)∠P=180°-![]() (∠B+∠D).
(∠B+∠D).
【解析】
(1)延长CO,交AP与B,根据三角形外角性质即可得答案;(2)根据2∠AOC=∠BAO +∠DCO+2∠P,2∠AOC=∠BAO +∠DCO+∠B+∠D,可得2∠P=∠B+∠D,进而可得答案;(3)由角平分线的定义可得∠PAB=∠PAD,∠PCB=∠PCE,根可三角形内角和定理可得2∠PAB+∠B=180°-2∠PCB+∠D,由(1)可知∠P=∠PAB+∠B+∠PCB,利用等量代换即可得答案;(4)由角平分线的定义可得∠FAP=∠PAD,∠PCE=∠PCB,根据四边形的内角和等于360°可得(180°-∠FAP)+∠P+∠PCB+∠B=360°,∠PAD+∠P+(180°-∠PCE)+∠D=360°,然后整理即可得解;
(1)如图,延长CO,交AP与B,
∵∠AOC=∠A+∠ABO,∠ABO=∠C+∠P,
∴∠AOC=∠A+∠P+∠C,
故答案为:∠AOC=∠A+∠P+∠C,

(2)∵2∠AOC =∠BAO +∠DCO+2∠P,2∠AOC=∠BAO +∠DCO+∠B+∠D,
∴2∠P=∠B+∠D,
∴∠P=![]() (28°+48°)=38°,
(28°+48°)=38°,
故答案为:38°
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°-2∠PCB+∠D,
∴180°-2(∠PAB+∠PCB)+∠D=∠B
∵∠P=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P-∠B,
∴180°-2(∠P-∠B)+∠D=∠B,即∠P=90°+![]() (∠B+∠D).
(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°-∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°-∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°-![]() (∠B+∠D).
(∠B+∠D).


科目:初中数学 来源: 题型:
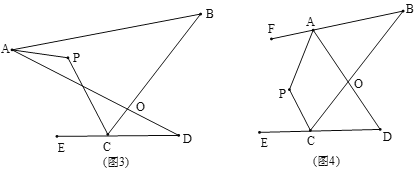
【题目】已知A,B,C,D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
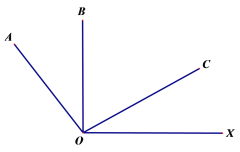
【题目】如图:已知OB⊥OX,OA⊥OC,∠COX=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转, 两条射线同时旋转,当一条射线与射线OX重合时,停止运动.
(1)开始旋转前,∠AOB=______________
(2)当OA与OC的夹角是10°时,求旋转的时间.
(3)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OX重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能公交车
型两种环保节能公交车![]() 辆,若购买
辆,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元,若购买
万元,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)求购买购买![]() 型和
型和![]() 型公交车每辆多少钱?
型公交车每辆多少钱?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为![]() 万人次和
万人次和![]() 万人次,若该公司购买
万人次,若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过
型公交车的总费用不超过![]() 万元,且确保这
万元,且确保这![]() 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于![]() 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
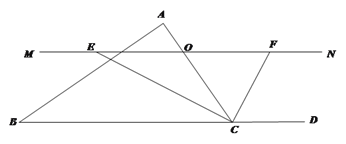
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
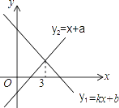
【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
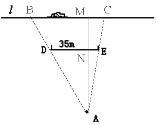
【题目】如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com