
【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能公交车
型两种环保节能公交车![]() 辆,若购买
辆,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元,若购买
万元,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)求购买购买![]() 型和
型和![]() 型公交车每辆多少钱?
型公交车每辆多少钱?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为![]() 万人次和
万人次和![]() 万人次,若该公司购买
万人次,若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过
型公交车的总费用不超过![]() 万元,且确保这
万元,且确保这![]() 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于![]() 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
【答案】(1)A型公交车100万元/辆,B型公交车150元/辆;(2)三种方案:①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆;(3)购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.
【解析】
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,根据“A型公交车1辆,B型公交车2辆,共需400万元;A型公交车2辆,B型公交车1辆,共需350万元”列出方程组解决问题;
(2)设购买A型公交车m辆,则B型公交车(10m)辆,由“购买A型和B型公交车的总费用不超过1200万元”和“10辆公交车在该线路的年均载客总和不少于680万人次”列出不等式组探讨得出答案即可;
(3)分别求出各种购车方案总费用,再根据总费用作出判断.
(1)设购买A型公交车x万元/辆,B型公交车y元/辆,
由题意,得![]() ,
,
解得![]() ,
,
答:A型公交车100万元/辆,B型公交车150元/辆;
(2)设A型公交车m辆,则B型公交车(10m)辆,
由题意,得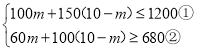 ,
,
解①,得m≥6;
解②,得m≤8;
解得6≤m≤8,
所以m=6,7,8,
则(10m)=4,3,2;
三种方案:①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆;
(3)①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
故购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.


科目:初中数学 来源: 题型:
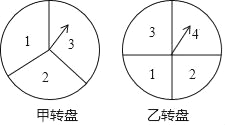
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一次函数
,一次函数![]() 的图像交
的图像交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .以
.以![]() 为圆心的⊙
为圆心的⊙![]() 与
与![]() 轴相切,若点
轴相切,若点![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移,同时⊙
轴向右平移,同时⊙![]() 的半径以每秒增加
的半径以每秒增加![]() 个单位的速度不断变大,设运动时间为
个单位的速度不断变大,设运动时间为![]() .
.
(![]() )点
)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,
的坐标为__________,![]() __________
__________![]() .
.
(![]() )在运动过程中,点
)在运动过程中,点![]() 的坐标为__________,⊙
的坐标为__________,⊙![]() 的半径为__________(用含
的半径为__________(用含![]() 的代数式表示).
的代数式表示).
(![]() )当⊙
)当⊙![]() 与直线
与直线![]() 相交于点
相交于点![]() 、
、![]() 时.
时.
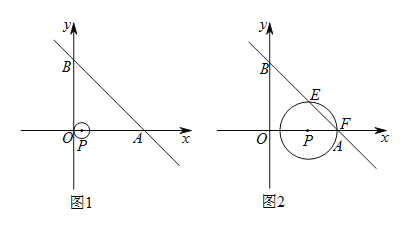
①如图![]() ,求
,求![]() 时弦
时弦![]() 的长.
的长.
②在运动过程中,是否存在以点![]() 为直角顶点的
为直角顶点的![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由(利用图
的值;若不存在,请说明理由(利用图![]() 解题).
解题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通常情况下,![]() 不一定等于
不一定等于![]() ,但我们数学上存在这样一些特殊的数对,观察:
,但我们数学上存在这样一些特殊的数对,观察:![]() ,
,![]() ,
,![]() ,…,我们把符合
,…,我们把符合![]() 的两个数叫做“和积数对”,已知
的两个数叫做“和积数对”,已知![]()
![]() 是一对“和积数对”.
是一对“和积数对”.
(1)请举出一对![]() 是“和积数对”,并验证其正确性;
是“和积数对”,并验证其正确性;
(2)求代数式![]() 的值;
的值;
(3)小明发现了一个关于![]() 的结论:
的结论:![]() ;你认为小明发现的结论正确吗?请说明理由.
;你认为小明发现的结论正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
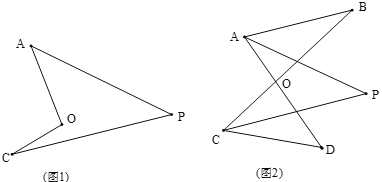
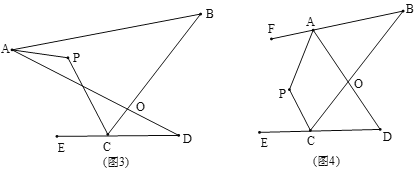
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
解决问题:
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
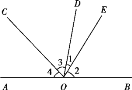
【题目】如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1.
(1)若∠1=18°,求∠COE的度数;
(2)若∠COE=70°,求∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
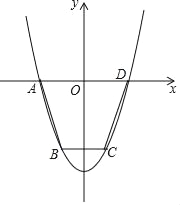
【题目】如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件20元的价格购进一批商品,如果以每件30元销售,那么半月内可售出400件.根据销售经验,销售单价每提高1元,半月内的销售量相应减少20件.如何提高销售单价,才能在半月内获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com