
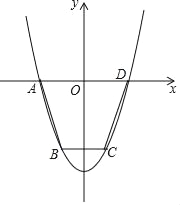
【题目】如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB.
(1)若∠B=86°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=![]() ∠DGC=
∠DGC=![]() 直接写出当
直接写出当![]() 满足什么数量关系时,AE∥DG?
满足什么数量关系时,AE∥DG?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能公交车
型两种环保节能公交车![]() 辆,若购买
辆,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元,若购买
万元,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)求购买购买![]() 型和
型和![]() 型公交车每辆多少钱?
型公交车每辆多少钱?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为![]() 万人次和
万人次和![]() 万人次,若该公司购买
万人次,若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过
型公交车的总费用不超过![]() 万元,且确保这
万元,且确保这![]() 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于![]() 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 长分别为32,42,52的线段组成的三角形是直角三角形
B. 连接对角线垂直的四边形各边中点所得的四边形是矩形
C. 一组对边平行且另一组对边相等的四边形是平行四边形
D. 对角线垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
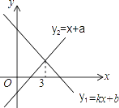
【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行杜拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com