【题目】下列命题中，是真命题的是( )
A. 长分别为32,42,52的线段组成的三角形是直角三角形
B. 连接对角线垂直的四边形各边中点所得的四边形是矩形
C. 一组对边平行且另一组对边相等的四边形是平行四边形
D. 对角线垂直且相等的四边形是正方形
阅读快车系列答案科目：初中数学 来源： 题型：
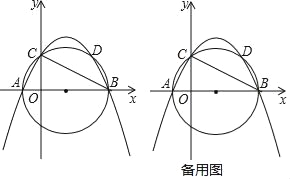
【题目】如图，已知二次函数y=ax2+bx+c（a＜0，c＞0）与x轴交于点A、B，与y轴交于点C，且以AB为直径的圆经过点C．
（1）若点A（﹣2，0），点B（8，0），求ac的值；
（2）若点A（x1，0），B（x2，0），试探索ac是否为定值？若是，求出这个定值；若不是，请说明理由．
（3）若点D是圆与抛物线的交点（D与 A、B、C 不重合），在（1）的条件下，坐标轴上是否存在一点P，使得以P、B、C为顶点的三角形与△CBD相似？若存在，请直接写出点P坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】通常情况下，
不一定等于
，但我们数学上存在这样一些特殊的数对，观察：
，
，
，…，我们把符合
的两个数叫做“和积数对”，已知
是一对“和积数对”．
（1）请举出一对是“和积数对”，并验证其正确性；
（2）求代数式
的值；
（3）小明发现了一个关于的结论：
；你认为小明发现的结论正确吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
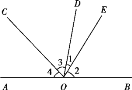
【题目】如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠2=3∠1.
（1）若∠1=18°，求∠COE的度数；
（2）若∠COE=70°，求∠2的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，点E、F、H分别是AB、BC、CD的中点，CE、DF交于G，连接AG、HG．下列结论：①CE⊥DF；②AG＝AD；③∠CHG＝∠DAG；④HG＝
AD．其中正确的有( )
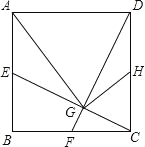
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
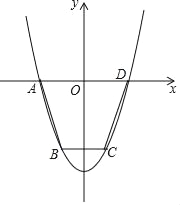
【题目】如图，抛物线y=ax2+c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（﹣2，0），B（﹣1，﹣3）．
（1）求抛物线的解析式；
（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与x轴交于点A，与y轴交于B，点P是x轴上的一个动点.
（1）求A、B两点的坐标；
（2）当点P在x轴正半轴上，且△APB的面积为8时，求直线PB的解析式；
（3）点Q在第二象限，是否存在以A、B、P、Q为顶点的四边形是菱形？若存在，请求出点Q的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，美丽的弦图，蕴含着四个全等的直角三角形．已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c．如图②，现将这四个全图②等的直角三角形紧密拼接，形成飞镖状，已知外围轮廓（实线）的周长为24，OC=3，则该飞镖状图案的面积（ ）
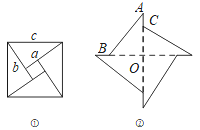
A. 6 B. 12 C. 24 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
