
【题目】如图,直线![]() 与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
(1)求A、B两点的坐标;
(2)当点P在x轴正半轴上,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.

【答案】(1)B(0,4),A(﹣3,0);(2)y=﹣x+4;(3)(﹣5,4)或(﹣![]() ,4)
,4)
【解析】
(1)根据坐标轴上点的特点即可得出结论;
(2)设出点P坐标,利用△PAB的面积建立方程求出P的坐标,最后用待定系数法求解即可;
(3)先判断出点Q在直线y=4上,再分两种情况讨论计算即可.
(1)令x=0时,y=4, ∴B(0,4),
令y=0时,![]() x+4=0,
x+4=0,
∴x=﹣3,
∴A(﹣3,0);
(2)设点P(m,0)(m>0), ∵A(﹣3,0),
∴AP=m﹣(﹣3)=m+3,
∵△APB的面积为8,
∴S△APB= ![]() AP×OB=
AP×OB=![]() (m+3)×4=8,
(m+3)×4=8,
∴m=1,
∴P(1,0),
∵B(0,4),
∴设直线PB的解析式为y=kx+4,
∴k+4=0,
∴k=﹣4,
∴直线PB的解析式为y=﹣x+4;
(3)如图,
∵以A、B、P、Q为顶点的四边形是菱形,且P在x轴上,
∴BQ∥AP,
∴点Q在直线y=4上,
由(1)知,A(﹣3,0),B(0,4),
∴AB=5,
∵点Q在第二象限内,
∴①当AB为菱形的边时,
∴BQ'=AB=5,
∴Q'(﹣5,4),
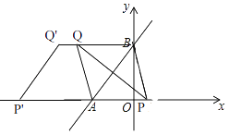
②当AB为菱形的对角线时,AB,PQ互相垂直平分,
∵直线AB的解析式为y= ![]() x+4,
x+4,
∴直线PQ的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
当y=4时,则﹣ ![]() x+
x+ ![]() =4,
=4,
∴x=﹣![]() ,
,
∴Q(﹣ ![]() ,4),
,4),
∴满足条件的点Q的坐标为(﹣5,4)或(﹣ ![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】某景区![]() 月
月![]() 日—
日—![]() 月
月![]() 日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游.
日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游.
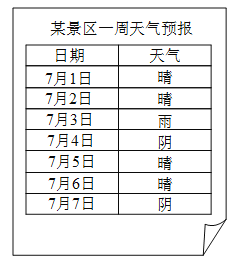
(![]() )随机选择一天,恰好天气预报是晴的概率是___________.
)随机选择一天,恰好天气预报是晴的概率是___________.
(![]() )求随机选择连续的两天,恰好天气预报都是晴的概率.
)求随机选择连续的两天,恰好天气预报都是晴的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 长分别为32,42,52的线段组成的三角形是直角三角形
B. 连接对角线垂直的四边形各边中点所得的四边形是矩形
C. 一组对边平行且另一组对边相等的四边形是平行四边形
D. 对角线垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额 | 人数(频数) | 频率 |
| 6 | 0.15 |
| 12 | 0.30 |
| 16 | 0.40 |
|
| 0.10 |
| 2 |
|

请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,![]() __________;
__________;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 轴于点(1,0),直线
轴于点(1,0),直线![]() 轴于点(2,0),直线
轴于点(2,0),直线![]() 轴于点(3,0),…,直线
轴于点(3,0),…,直线![]() 轴于点(n,0)。函数
轴于点(n,0)。函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() ;函数
;函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() 。如果
。如果![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,…,四边形
,…,四边形![]() 的面积记作
的面积记作![]() ,那么
,那么![]() _____________.
_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
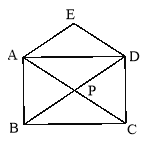
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com