
【题目】如图,直线![]() 轴于点(1,0),直线
轴于点(1,0),直线![]() 轴于点(2,0),直线
轴于点(2,0),直线![]() 轴于点(3,0),…,直线
轴于点(3,0),…,直线![]() 轴于点(n,0)。函数
轴于点(n,0)。函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() ;函数
;函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() 。如果
。如果![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,…,四边形
,…,四边形![]() 的面积记作
的面积记作![]() ,那么
,那么![]() _____________.
_____________.

【答案】![]()
【解析】
先求出A1,A2,A3,…An和点B1,B2,B3,…Bn的坐标,利用三角形的面积公式计算△OA1B1的面积;四边形A1A2B2B1的面积,四边形A2A3B3B2的面积,…四边形An-1AnBnBn-1的面积,则通过两个三角形的面积差计算,这样得到Sn=n-![]() ,然后把n=2019代入即可求得答案.
,然后把n=2019代入即可求得答案.
∵函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An,
∴A1(1,1),A2(2,2),A3(3,3)…An(n,n),
又∵函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn,
∴B1(1,2),B2(2,4),B3(3,6),…Bn(n,2n),
∴S1=![]() ×1×(2-1),
×1×(2-1),
S2=![]() ×2×(4-2)-
×2×(4-2)-![]() ×1×(2-1),
×1×(2-1),
S3=![]() ×3×(6-3)-
×3×(6-3)-![]() ×2×(4-2),
×2×(4-2),
…
Sn=![]() ×n(2n-n)-
×n(2n-n)-![]() ×(n-1)[2(n-1)-(n-1)]=
×(n-1)[2(n-1)-(n-1)]=![]() ×n2-
×n2-![]() ×(n-1)2=n-
×(n-1)2=n-![]() .
.
当n=2019,S2019=2019-![]() ×=2018
×=2018![]() .
.
故答案为:2018![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
(1)求A、B两点的坐标;
(2)当点P在x轴正半轴上,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件20元的价格购进一批商品,如果以每件30元销售,那么半月内可售出400件.根据销售经验,销售单价每提高1元,半月内的销售量相应减少20件.如何提高销售单价,才能在半月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
解:根据算术平方根的定义,
由![]() ,得
,得![]() ,所以
,所以![]() ①……第一步
①……第一步
根据立方根的定义,
由![]() ,得
,得![]() ②……第二步
②……第二步
由①②解得![]() ……第三步
……第三步
把![]() 代入
代入![]() 中,得
中,得![]() ……第四步
……第四步
(1)以上解题过程存在错误,请指出错在哪些步骤,并说明错误的原因;
(2)把正确解答过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积( )
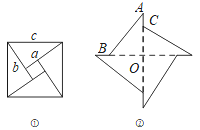
A. 6 B. 12 C. 24 D. 24![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com