
【题目】如图![]() ,一次函数
,一次函数![]() 的图像交
的图像交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .以
.以![]() 为圆心的⊙
为圆心的⊙![]() 与
与![]() 轴相切,若点
轴相切,若点![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移,同时⊙
轴向右平移,同时⊙![]() 的半径以每秒增加
的半径以每秒增加![]() 个单位的速度不断变大,设运动时间为
个单位的速度不断变大,设运动时间为![]() .
.
(![]() )点
)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,
的坐标为__________,![]() __________
__________![]() .
.
(![]() )在运动过程中,点
)在运动过程中,点![]() 的坐标为__________,⊙
的坐标为__________,⊙![]() 的半径为__________(用含
的半径为__________(用含![]() 的代数式表示).
的代数式表示).
(![]() )当⊙
)当⊙![]() 与直线
与直线![]() 相交于点
相交于点![]() 、
、![]() 时.
时.
①如图![]() ,求
,求![]() 时弦
时弦![]() 的长.
的长.
②在运动过程中,是否存在以点![]() 为直角顶点的
为直角顶点的![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由(利用图
的值;若不存在,请说明理由(利用图![]() 解题).
解题).
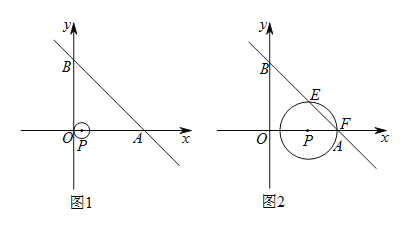
【答案】(1)(10,0),(0,10),45;(2)(1+2t,0),1+t;(3)①![]() ;②
;②![]() 或t=10.
或t=10.
【解析】试题分析:(1)利用待定系数法求出点A、B的坐标,即可解决问题.
(2)根据题意可得P(1+2t,0),⊙O半径为1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.在Rt△APK中,由∠PKA=90°,∠PAK=45°,PA=4,推出PK的值,在Rt△PEK中,根据勾股定理计算即可.
②分两种情形a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°;b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.分别列出方程求解即可.
试题解析:解:(1)∵y=﹣x+10的图象交x轴于点A,交y轴于点B,∴A(10,0),B(0,10),∴OA=OB=10.∵∠AOB=90°,∴∠OAB=∠OBA=45°.故答案分别为(10,0),(0,10),45°.
(2)由题意得:P(1+2t,0),⊙O半径为1+t.故答案为:(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
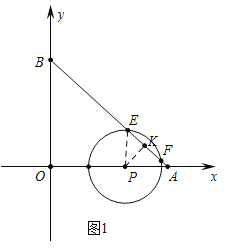
当t=![]() 时,P(6,0),半径为3.5,在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,∴PK=
时,P(6,0),半径为3.5,在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,∴PK=![]() PA=
PA=![]() ,在Rt△PEK中,EK=
,在Rt△PEK中,EK=![]() =
=![]() ,∴EF=2EK=
,∴EF=2EK=![]() .
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°.
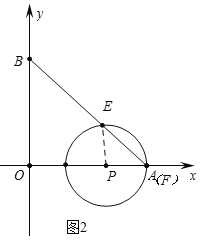
∵OP+PA=OA,∴1+2t+1+t=10,∴t=![]() .
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
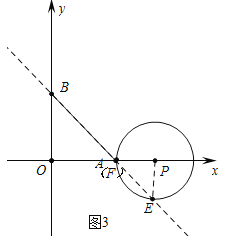
由OP﹣PF=OA,∴1+2t﹣(1+t)=10,∴t=10.
综上所述,t=![]() s或10s时,存在以点P为直角顶点的Rt△PEF.
s或10s时,存在以点P为直角顶点的Rt△PEF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________, ![]() =________%,
=________%, ![]() =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在下面平面直角坐标系中,已知A ![]() ,B
,B ![]() ,C
,C ![]() 三点.其中
三点.其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]()
![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积为△
的面积为△![]() 的面积的两倍?若存在,求出点
的面积的两倍?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB.
(1)若∠B=86°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=![]() ∠DGC=
∠DGC=![]() 直接写出当
直接写出当![]() 满足什么数量关系时,AE∥DG?
满足什么数量关系时,AE∥DG?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区![]() 月
月![]() 日—
日—![]() 月
月![]() 日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游.
日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游.
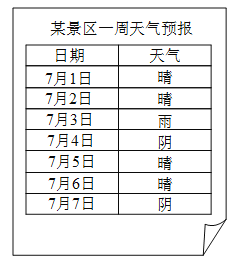
(![]() )随机选择一天,恰好天气预报是晴的概率是___________.
)随机选择一天,恰好天气预报是晴的概率是___________.
(![]() )求随机选择连续的两天,恰好天气预报都是晴的概率.
)求随机选择连续的两天,恰好天气预报都是晴的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
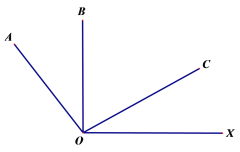
【题目】如图:已知OB⊥OX,OA⊥OC,∠COX=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转, 两条射线同时旋转,当一条射线与射线OX重合时,停止运动.
(1)开始旋转前,∠AOB=______________
(2)当OA与OC的夹角是10°时,求旋转的时间.
(3)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OX重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能公交车
型两种环保节能公交车![]() 辆,若购买
辆,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元,若购买
万元,若购买![]() 型公交车
型公交车![]() 辆,
辆,![]() 型公交车
型公交车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)求购买购买![]() 型和
型和![]() 型公交车每辆多少钱?
型公交车每辆多少钱?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为![]() 万人次和
万人次和![]() 万人次,若该公司购买
万人次,若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过
型公交车的总费用不超过![]() 万元,且确保这
万元,且确保这![]() 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于![]() 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com