
【题目】甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).
【答案】
(1)解:设甲服装的进价为x元,则乙服装的进价为(500﹣x)元,
根据题意得:90%(1+30%)x+90%(1+20%)(500﹣x)﹣500=67,
解得:x=300,
500﹣x=200.
答:甲服装的进价为300元、乙服装的进价为200元.
(2)解:∵乙服装的进价为200元,经过两次上调价格后,使乙服装每件的进价达到242元,
∴设每件乙服装进价的平均增长率为y,
则200(1+y) 2=242,
解得:y1=0.1=10%,y2=﹣2.1(不合题意舍去).
答:每件乙服装进价的平均增长率为10%
(3)解:∵每件乙服装进价按平均增长率再次上调,
∴再次上调价格为:242×(1+10%)=266.2(元),
∵商场仍按9折出售,设定价为a元时,
0.9a﹣266.2>0,
解得:a> ![]() .
.
故定价至少为296元时,乙服装才可获得利润.
【解析】(1)若设甲服装的进价为x元,则乙服装的进价为(500﹣x)元.根据公式:总利润=总售价﹣总进价,即可列出方程.(2)利用乙服装的进价为200元,经过两次上调价格后,使乙服装每件的进价达到242元,利用增长率公式求出即可;(3)利用每件乙服装进价按平均增长率再次上调,再次上调价格为:242×(1+10%)=266.2(元),进而利用不等式求出即可.


科目:初中数学 来源: 题型:
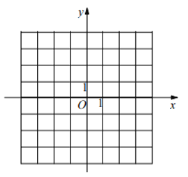
【题目】在直角坐标平面内,已知点![]() ,将点
,将点![]() 向右平移5个单位得到点
向右平移5个单位得到点![]()
(1)描出点![]() 的位置,并求
的位置,并求![]() 的面积.
的面积.
(2)若在![]() 轴下方有一点
轴下方有一点![]() ,使
,使![]() ,写出一个满足条件的点
,写出一个满足条件的点![]() 的坐标.并指出满足条件的点
的坐标.并指出满足条件的点![]() 有什么特征.
有什么特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
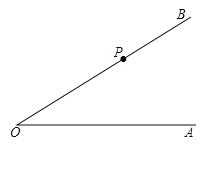
【题目】按照下列要求画图并填空:
如图,点![]() 是
是![]() 的边
的边![]() 上的一点,
上的一点,
(1)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)在(1)的基础上作![]() 的边
的边![]() 上的高,垂足为
上的高,垂足为![]() ;
;
(3)线段___________的长度是点![]() 到直线
到直线![]() 的距离;
的距离;
(4)线段![]() 这三条线段大小关系是___________(用“<”号连接).
这三条线段大小关系是___________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,完成下列问题:
,完成下列问题:
(1)求此函数图像与x轴、y轴的交点坐标;
(2)画出此函数的图像;观察图像,当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)平移一次函数![]() 的图像后经过点(-3,1),求平移后的函数表达式.
的图像后经过点(-3,1),求平移后的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)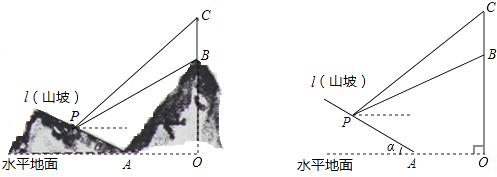
查看答案和解析>>
科目:初中数学 来源: 题型:
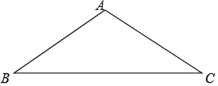
【题目】如图,△ABC中,AB=AC,∠A=108°.
(1)实践与操作:作AB的垂直平分线DE,与AB,BC分别交于点D,E(用尺规作图.保留作图痕迹,不要求写作法)
(2)推理与计算:求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( ) 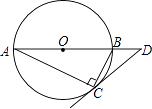
A.25°
B.40°
C.50°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
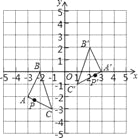
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何证明:
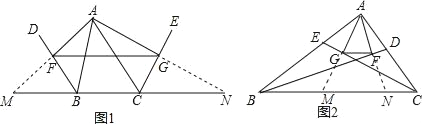
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com