
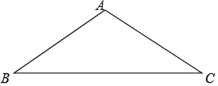
【题目】如图,△ABC中,AB=AC,∠A=108°.
(1)实践与操作:作AB的垂直平分线DE,与AB,BC分别交于点D,E(用尺规作图.保留作图痕迹,不要求写作法)
(2)推理与计算:求∠AEC的度数.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:

(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数 ![]() 图象于点A,B,交x轴于点C.
图象于点A,B,交x轴于点C.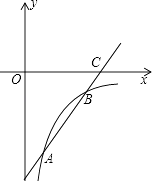
(1)求m的取值范围;
(2)若点A的坐标是(1,﹣4),且 ![]() ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;
(3)在(2)的情况下,请直接写出不等式 ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
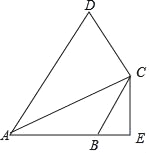
【题目】如图,在四边形ABCD中,AC平分∠DAB,∠D+∠ABC=180°,CE⊥AB,垂足为E,若△ACD和△ABC的面积分别为50和38,则△CBE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A.a<13,b=13
B.a<13,b<13
C.a>13,b<13
D.a>13,b=13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得: ![]() 的值为常数t,则t= .
的值为常数t,则t= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com