
【题目】如图,已知一次函数y=kx+b的图象交反比例函数 ![]() 图象于点A,B,交x轴于点C.
图象于点A,B,交x轴于点C.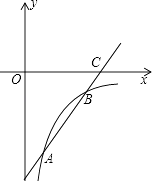
(1)求m的取值范围;
(2)若点A的坐标是(1,﹣4),且 ![]() ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;
(3)在(2)的情况下,请直接写出不等式 ![]() 的解集.
的解集.
【答案】
(1)解:因为反比例函数 ![]() 的图象在第四象限,
的图象在第四象限,
所以4﹣2m<0,解得m>2.
(2)解:因为点A(1,﹣4)在函数 ![]() 图象上,
图象上,
所以﹣4=4﹣2m,解得m=4.
过点A、B分别作AM⊥OC于点M,BN⊥OC于点N,
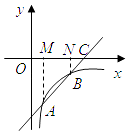
所以∠BNC=∠AMC=90°,
又因为∠BCN=∠ACM,
所以△BCN∽△ACM,所以 ![]() .
.
因为 ![]() ,所以
,所以 ![]() ,即
,即 ![]() .
.
因为AM=4,所以BN=1.
所以点B的纵坐标是﹣1.
因为点B在反比例函数 ![]() 的图象上,所以当y=﹣1时,x=4.
的图象上,所以当y=﹣1时,x=4.
所以点B的坐标是(4,﹣1).
因为一次函数y=kx+b的图象过点A(1,﹣4)、B(4,﹣1),
所解得 ![]() ,
,
解得:k=1,b=﹣5
所以一次函数的解析式是y=x﹣5;
(3)解:由函数图象可知不等式 ![]() 的解集为:0<x<1 或 x>4.
的解集为:0<x<1 或 x>4.
【解析】(1)根据双曲线位于第四象限可得到比例系数k<0,即4-2m<0,然后解关于m的不等式即可;
(2)先把点A的坐标代入反比例函数表达式客求出m的值,接下来,再证明△BCN∽△ACM,依据相似三角形的性质可求得BN=1,然后将y=-1代入反比例函数的解析式可求得点B的横坐标,最后由点A和点B的坐标可求得直线AB的解析式;
(3)依据函数图像确定出一次函数图像位于反比例函数图像上方时,自变量的取值范围即可.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )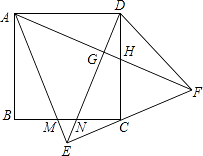
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照下列要求画图并填空:
如图,点![]() 是
是![]() 的边
的边![]() 上的一点,
上的一点,
(1)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)在(1)的基础上作![]() 的边
的边![]() 上的高,垂足为
上的高,垂足为![]() ;
;
(3)线段___________的长度是点![]() 到直线
到直线![]() 的距离;
的距离;
(4)线段![]() 这三条线段大小关系是___________(用“<”号连接).
这三条线段大小关系是___________(用“<”号连接).
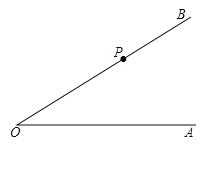
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,完成下列问题:
,完成下列问题:
(1)求此函数图像与x轴、y轴的交点坐标;
(2)画出此函数的图像;观察图像,当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)平移一次函数![]() 的图像后经过点(-3,1),求平移后的函数表达式.
的图像后经过点(-3,1),求平移后的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=108°.
(1)实践与操作:作AB的垂直平分线DE,与AB,BC分别交于点D,E(用尺规作图.保留作图痕迹,不要求写作法)
(2)推理与计算:求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.
(1)求出点C,D的坐标;
(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组![]() 有正整数解,求点P的坐标;
有正整数解,求点P的坐标;
(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ的值不小于0.6且不大于4,求n的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com