
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )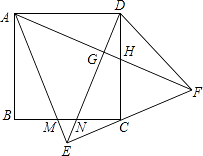
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】解:如图,连接AC、以D为圆心DA为半径画圆.
∵四边形ABCD是正方形,
∴DA=DC=AB=BC,∠ADC=∠B=∠DCB=90°,∠ACD=∠DAC=45°
∵△DEF是由△DEA翻折得到,
∴DA=DF=DC,EA=EF,∠AED=∠DEF,
∴∠AFC= ![]() ∠ADC=45°
∠ADC=45°
∴∠EFA=∠EAF=45°,
∴∠AEF=90°,
∴∠DEF=∠DEA=45°,
∵EA=ED=EF,
∴∠DAE=∠ADE=∠EDF=∠EFD=67.5°,
∴∠DAF=∠DFA=22.5°,
∴∠ADF=180°﹣∠DAF﹣∠DFA=135°,
∴∠CDF=∠ADF﹣∠ADC=45°,
∴∠DCF=180°﹣∠CDF﹣∠DFC=67.5°,
∵∠CHF=∠CDF+∠DFA=67.5°,
∴∠HCF=∠FHC,
∴△CFH是等腰三角形,故③正确.②错误,
∵∠ACD=∠CDF,
∴AC∥DF,
∴S△DFA=S△FDC,
∴S△ADH=S△CHF,故⑤正确,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠BAM=∠CDN,
在△ABM和△DCN中,
 ,
,
∴△ABM≌△DCN,故①正确,
在△EAF中,∵∠CAE=∠CAF,∠AEC=90°,作CK⊥AF于K,
∴CE=CK<CF,
∴CE≠CF故④错误.
∴①③⑤正确,
选B.

【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF. 
(1)求证:EF是⊙O的切线;
(2)小强同学通过探究发现:AF+CF=2AO,请你帮助小强同学证明这一结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:

(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
B.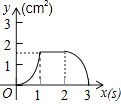
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,四边形DECF为正方形,回答下列问题.
(1)简述图1经过怎样的变换可形成图2?
(2)若AD=3,BD=4,求△ADE与△BDF的面积之和.
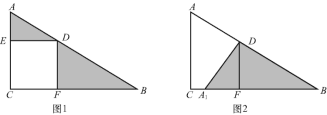
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() .
.

(1)填空:![]() _____,
_____,![]() ______,
______,![]() _______;
_______;
(2)点![]() 为射线
为射线![]() 上一任意一点,连接
上一任意一点,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,交射线
,交射线![]() 于点
于点![]() ,作
,作![]() 的平分线
的平分线![]() ,交直线
,交直线![]() 于点
于点![]() ,请探究射线
,请探究射线![]() 与
与![]() 之间的位置关系,并加以证明;
之间的位置关系,并加以证明;
(3)连接![]() ,若
,若![]() 恰好平分
恰好平分![]() ,则在(2)问的条件下,是否存在角度
,则在(2)问的条件下,是否存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数)?若存在,求出
为不超过10的正整数)?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数 ![]() 图象于点A,B,交x轴于点C.
图象于点A,B,交x轴于点C.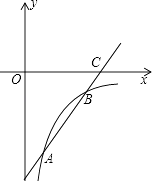
(1)求m的取值范围;
(2)若点A的坐标是(1,﹣4),且 ![]() ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;
(3)在(2)的情况下,请直接写出不等式 ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com