
【题目】如图,在Rt△ACB中,四边形DECF为正方形,回答下列问题.
(1)简述图1经过怎样的变换可形成图2?
(2)若AD=3,BD=4,求△ADE与△BDF的面积之和.
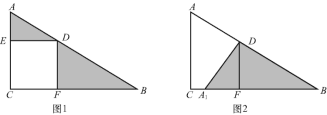
【答案】(1)把△ADE绕D点逆时针旋转90°得△A1DF;(2)6.
【解析】
(1)观察图形,发现DA旋转到DA1,DE旋转到DF,而∠EDF=90°,由旋转的定义即可描述由图(1)变成图(2)的形成过程;
(2)由图形的旋转可知,图形顺时针旋转了90°,即∠EDF=∠ADA1=90°,可得∠A1DB=90°,△ADE和△BDF面积的和即为△A1DB的面积.
(1)由题意可得,把△ADE绕D点逆时针旋转90°得△A1DF.
(2)由图及(1)知S△ADE+S△BDF=![]() ,
,
根据图形的旋转性质可知AD=A1D,∠ADE=∠A1DF,
又∵∠ADE+∠FDB=90°,
∴∠A1DF+∠FDB=90°,即∠A1DB=90°.
∴在Rt△A1DB中,A1D=AD=3,BD=4,
![]() A1D×BD=6,
A1D×BD=6,
∴△ADE与△BDF面积之和为6.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,P为x轴正半轴一动点,BC平分
,P为x轴正半轴一动点,BC平分![]() ,PC平分
,PC平分![]() ,OD平分
,OD平分![]()
![]() 求
求![]() 的度数;
的度数;
![]() 求证:
求证:![]() ;
;
![]() 在运动中,
在运动中,![]() 的值是否变化?若发生变化,说明理由;若不变,求其值.
的值是否变化?若发生变化,说明理由;若不变,求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
A.24﹣4π
B.32﹣4π
C.32﹣8π
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )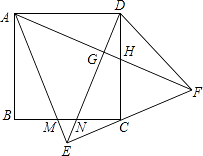
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
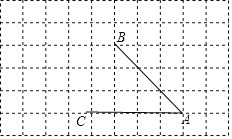
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线 的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com