
【题目】如图,在平面直角坐标系中,![]() ,P为x轴正半轴一动点,BC平分
,P为x轴正半轴一动点,BC平分![]() ,PC平分
,PC平分![]() ,OD平分
,OD平分![]()
![]() 求
求![]() 的度数;
的度数;
![]() 求证:
求证:![]() ;
;
![]() 在运动中,
在运动中,![]() 的值是否变化?若发生变化,说明理由;若不变,求其值.
的值是否变化?若发生变化,说明理由;若不变,求其值.

【答案】![]() 30°;
30°;![]() 证明见解析;
证明见解析;![]() 不变,105°.
不变,105°.
【解析】
(1)在Rt△AOB中根据已知和两锐角互余的性质即可求出∠BAO的度数;
(2)根据外角的性质表示出∠C,得到∠C与∠OAP之间的数量关系;
(3)根据对顶角相等,分别表示出∠C和∠D,得到∠C+∠D的值.
![]() ∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∴2∠BAO+∠BAO+90°=180°,
∴∠BAO=30°;
![]() ∵∠CBP=
∵∠CBP=![]() ∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∴∠CBP=30°,
∵∠CPF=∠C+∠CBP,∠APF=∠OAP+∠AOP,∠CPF=![]() ∠APF,
∠APF,
∴∠C+∠CBP=![]() (∠OAP+∠AOP),
(∠OAP+∠AOP),
∵∠AOP=90°,
∴∠C+30°=![]() (∠OAP+90°)=
(∠OAP+90°)=![]() ∠OAP+45°,
∠OAP+45°,
∴∠C=15°+![]() ∠OAP;
∠OAP;
![]() 不变,
不变,
∵∠D+∠DOP+∠OPD=180°,∠DOP=![]() ∠EOF=
∠EOF=![]() ×90°=45°,
×90°=45°,
∴∠D+45°+∠OPD=180°,
∵∠OPD=∠C+∠CBP,
∴∠D+45°+∠C+∠CBP=180°,
∵∠CBP=30°,
∴∠D+∠C=180°-45°-∠CBP=135°-30°=105°,
∴∠D+∠C=105°,保持不变.


科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
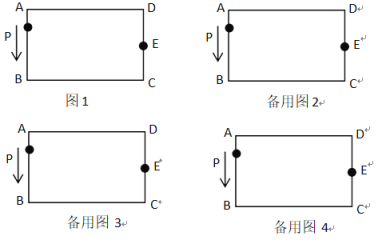
【题目】如图,长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A B C E运动到E点停止,设点P经过的路程为![]() ,APE的面积为
,APE的面积为![]() .
.
(1)当![]() 时,在图1中画出草图,并求出对应
时,在图1中画出草图,并求出对应![]() 的值;
的值;
(2)利用备用图画出草图,写出![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述不正确的是( )
A. 一个三角形必有三条中位线
B. 一个三角形必有三条中线
C. 三角形的一条中线分成的两个三角形的面积相等
D. 三角形的一条中位线分成的两部分面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入它所属于的集合的括号内.
9,![]() ,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
正分数集合{_________}
负分数集合{_________}
负整数集合{__________}
非负整数集合{________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根. 其中正确的结论是( )
A.③④
B.②④
C.②③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一天数学老师布置了一道数学题:已知x=2017,求整式![]() 的值,小明观察后提出:“已知x=2017是多余的”,你认为小明的说法有道理吗?请解释.
的值,小明观察后提出:“已知x=2017是多余的”,你认为小明的说法有道理吗?请解释.
(2)已知整式![]() ,整式M与整式N之差是
,整式M与整式N之差是![]() .
.
①求出整式N.
②若a是常数,且2M+N的值与x无关,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
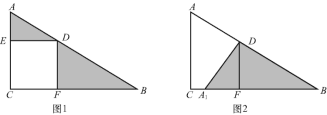
【题目】如图,在Rt△ACB中,四边形DECF为正方形,回答下列问题.
(1)简述图1经过怎样的变换可形成图2?
(2)若AD=3,BD=4,求△ADE与△BDF的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com