
【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根. 其中正确的结论是( )
A.③④
B.②④
C.②③
D.①④
【答案】A
【解析】解:∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以①错误;
∵抛物线y=ax2+bx+c的顶点D(﹣1,2),
∴抛物线的对称轴为直线x=﹣1,
而抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点A在点(0,0)和(1,0)之间,
∴x=1时,y<0,
∴a﹣b+c<0,所以②错误;
∵抛物线的对称轴为直线x=﹣ ![]() =﹣1,
=﹣1,
∴b=2a,
∵x=﹣1时,y=2,
即a﹣b+c=2,
∴a﹣2a+c=2,即c﹣a=2,所以③正确;
∵抛物线y=ax2+bx+c的顶点D(﹣1,2),
即x=﹣1时,y有最大值2,
∴抛物线与直线y=2只有一个公共点,
∴方程ax2+bx+c﹣2=0有两个相等的实数根,所以④正确.
故选A.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;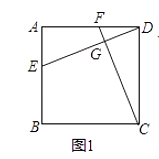
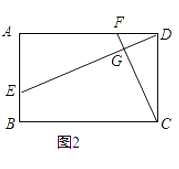
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: ![]() =
= ![]() ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.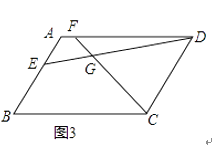
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,P为x轴正半轴一动点,BC平分
,P为x轴正半轴一动点,BC平分![]() ,PC平分
,PC平分![]() ,OD平分
,OD平分![]()
![]() 求
求![]() 的度数;
的度数;
![]() 求证:
求证:![]() ;
;
![]() 在运动中,
在运动中,![]() 的值是否变化?若发生变化,说明理由;若不变,求其值.
的值是否变化?若发生变化,说明理由;若不变,求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
A.24﹣4π
B.32﹣4π
C.32﹣8π
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com