
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;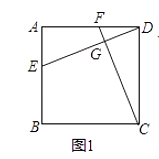
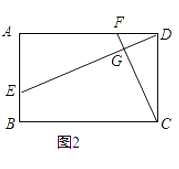
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: ![]() =
= ![]() ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.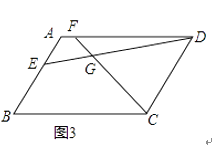
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,
∴∠AED=∠CFD,
∴△ADE≌△DCF,
∴DE=CF
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,∠DCF+∠CFD=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴ ![]() =
= ![]()
(3)解:当∠B=∠EGF时, ![]() =
= ![]() 成立,
成立,
证明:如图3,在AD的延长线上取点M,使CM=CF,
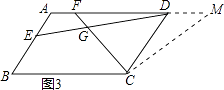
则∠CMF=∠CFM,
∵AB∥CD,
∴∠A=∠CDM,
∵AD∥BC,
∴∠B+∠A=180°,
∵∠B=∠EGF,
∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
【解析】(1)依据正方形的性质可得到∠A=∠ADC=90°,AD=DC,然后再依据同角的余角相等可证明∠AED=∠CFD,最后,在依据AAS证明△ADE≌△DCF,最后,利用全等三角形对应边相等进行证明即可;
(2)依据矩形的性质可得到∠A=∠ADC=90°,然后再依据同角的余角相等可证明∠ADE=∠DCF,接下来,利用两对角相等的三角形相似得到三角形ADE与三角形DCF相似,最后,利用相似三角形对应边成比例进行证明即可;
(3)在AD的延长线上取点M,使CM=CF,先证明△ADE∽△DCM,然后再利用相似三角形对应边成比例进行证明即可.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= ![]() 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )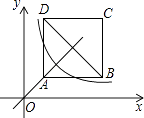
A.1<k<9
B.2≤k≤34
C.1≤k≤16
D.4≤k<16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
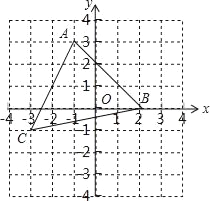
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为__________.
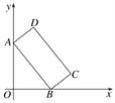
查看答案和解析>>
科目:初中数学 来源: 题型:
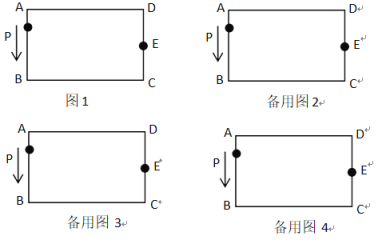
【题目】如图,长方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A B C E运动到E点停止,设点P经过的路程为![]() ,APE的面积为
,APE的面积为![]() .
.
(1)当![]() 时,在图1中画出草图,并求出对应
时,在图1中画出草图,并求出对应![]() 的值;
的值;
(2)利用备用图画出草图,写出![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根. 其中正确的结论是( )
A.③④
B.②④
C.②③
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com