
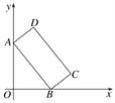
【题目】如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为__________.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】一个三位自然数是![]() ,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数
,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数![]() (
(![]() 可以与
可以与![]() 相同),设
相同),设![]() ,在
,在![]() 所有的可能情况中,当
所有的可能情况中,当![]() 最大时,我们称此时的
最大时,我们称此时的![]() 是
是![]() 的“梦想数”,并规定
的“梦想数”,并规定![]() .例如127按上述方法可得到新数有:217、172、721,因为
.例如127按上述方法可得到新数有:217、172、721,因为![]() 所以172是172的“梦想数”,此时,
所以172是172的“梦想数”,此时,![]() .
.
(1)求512的“梦想数”及![]() 的值;
的值;
(2)设三位自然数![]() 交换其个位与十位上的数字得到新数
交换其个位与十位上的数字得到新数![]() ,若
,若![]() ,且
,且![]() 能被7整除,求
能被7整除,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;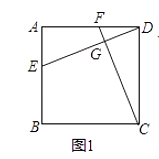
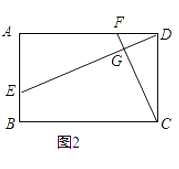
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: ![]() =
= ![]() ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.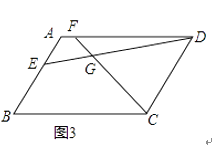
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江苏省无锡市)某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本p(万元)与销售额y(万元)之间函数关系的图象图2中线段AB所示.

(1)求经销成本p(万元)与销售额y(万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额﹣经销成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= ![]() 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.
相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.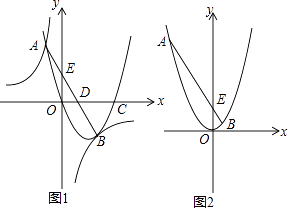
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com