
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 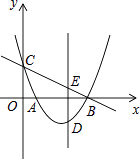
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83;乙:88,79,90,81,72.
请回答下列问题:
(1)甲成绩的平均数是______,乙成绩的平均数是______;
(2)经计算知![]() =6,
=6,![]() =42,你认为选谁参加比赛更合适,说明理由.
=42,你认为选谁参加比赛更合适,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.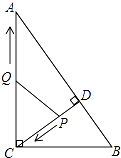
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
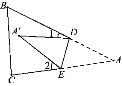
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【定义】已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外),那么就称P为△ABC的“共相似点”,根据“共相似点”是否落在三角形的内部,边上或外部,可将其分为“内共相似点”,“边共相似点”或“外共相似点”.
(1)据定义可知,等边三角形(填“存在”或“不存在”)共相似点.
(2)如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
(3)如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
(4)如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC= ![]() ,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 .
,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+ ![]() ﹣
﹣ ![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,ABCD是菱形?
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com