Question

【题目】【定义】已知P为△ABC所在平面内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，若存在一个三角形与△ABC相似（全等除外），那么就称P为△ABC的“共相似点”，根据“共相似点”是否落在三角形的内部，边上或外部，可将其分为“内共相似点”，“边共相似点”或“外共相似点”．
（1）据定义可知，等边三角形（填“存在”或“不存在”）共相似点．
（2）如图1，若△ABC的一个边共相似点P与其对角顶点B的连线，将△ABC分割成的两个三角形恰与原三角形均相似，试判断△ABC的形状，并说明理由．

（3）如图2，在△ABC中，∠A＜∠B＜∠C，高线CD与角平分线BE交于点P，若P是△ABC的一个内共相似点，试说明点E是△ABC的边共相似点，并直接写出∠A的度数．

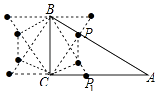
（4）如图3，在Rt△ABC中，∠C=90°，∠A=30°，BC= ，若△PBC与△ABC相似，则满足条件的P点共有个，顺次连接所有满足条件的P点而围成的多边形的周长为 ．

Answer 1

【答案】
（1）不存在
（2）

解：△ABC是直角三角形，理由如下：

根据题意得：△ABP∽△ACB，

∴∠ABP=∠C，

同理得：∠CBP=∠A，

∴∠ABC=∠A+∠C=180°﹣∠ABC，

解得：∠ABC=90°，

∴△ABC是直角三角形；

（3）

解：根据题意得：△PBC∽△CAB，

∴∠PBC=∠A，∠PCB=∠ABC，

∵BE平分∠ABC，

∴∠ABE=∠PBC，

∴∠A=∠ABE=∠PBC，

∴∠PCB=∠ABC=2∠A=2∠PBC，

∵∠BCE=∠ACB，∠PBC=∠A，

∴△BEC∽△ABC，

∴点E是△ABC的边共相似点；

∵CD是△ABC的高，

∴∠CDB=90°，

∴∠PCB+∠ABC=90°，

∴2∠A+2∠A=90°，

解得：∠A=22.5°；

（4）8；6+
【解析】解：（1）根据“共相似点”的定义得：等边三角形不存在共相似点．
所以答案是：不存在；
4）作CP⊥AB于P，则P为△ABC的“共相似点”；
过B作BC的垂线与CP的延长线的交点是△ABC的“共相似点”；
作∠ABC的平分线与AC的交点P1是△ABC的“共相似点”；
过C作BP1的垂线，垂足是△ABC的“共相似点”；
同理：以上四个△ABC的“共相似点”关于直线BC的对称点是△ABC的“共相似点”；
∴△ABC的“共相似点”共有8个，如图所示：
根据等边三角形的性质和直角三角形的性质得：顺次连接所有满足条件的P点而围成的多边形的周长为 2×2+4× +2× =6+ ；
所以答案是：8；6+ ．

【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．