
【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+ ![]() ﹣
﹣ ![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,ABCD是菱形?
(2)若AB的长为2,那么ABCD的周长是多少?
【答案】
(1)解:∵ABCD是菱形,
∴AB=AD,
∴△=b2﹣4ac=(﹣m)2﹣4×1×( ![]() ﹣
﹣ ![]() )
)
=m2﹣2m+1
=(m﹣1)2=0,
解得:m=1,
即m为1时,ABCD是菱形
(2)解:把AB=2代入方程得:
4﹣2m+ ![]() ﹣
﹣ ![]() =0,
=0,
解得:m= ![]() ,
,
则x2﹣ ![]() x+1=0,
x+1=0,
解得:x1= ![]() ,x2=2,
,x2=2,
则AD= ![]() ,
,
故ABCD的周长是:2×(2+ ![]() )=5
)=5
【解析】(1)直接利用菱形性质结合根的判别式求出m的值;(2)利用AB=2,代入方程求出m的值,进而解方程得出x的值,再利用平行四边形的性质得出答案.
【考点精析】利用平行四边形的性质和菱形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 3(m-1) B. ![]() (m-2) C. 1 D. 3
(m-2) C. 1 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H. 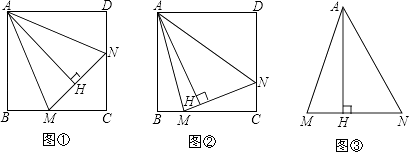
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报,然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,试求:
(1)小明回家的速度.
(2)小明离家50分钟时离家的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若函数y=kx﹣3的图象如图所示,则一元二次方程x2+x+k﹣1=0根的存在情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图①,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了图②,如果继续“生长”下去 ,它将变得“枝繁叶茂”,则“生长”了2 014次后形成的图形中所有正方形的面积和是( )

A. 2 012 B. 2 013 C. 2 014 D. 2 015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com