
【题目】若函数y=kx﹣3的图象如图所示,则一元二次方程x2+x+k﹣1=0根的存在情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
【答案】A
【解析】解:根据函数y=kx﹣3的图象可得k<0,
则一元二次方程x2+x+k﹣1=0中,△=12﹣4×1×(k﹣1)=5﹣4k>0,
则一元二次方程x2+x+k﹣1=0根的存在情况是有两个不相等的实数根,
故选:A.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


科目:初中数学 来源: 题型:
【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
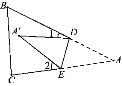
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论: ① ![]() ;②∠ADF=∠CDB;③点F是GE的中点;④AF=
;②∠ADF=∠CDB;③点F是GE的中点;④AF= ![]() AB;⑤S△ABC=5S△BDF ,
AB;⑤S△ABC=5S△BDF ,
其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+ ![]() ﹣
﹣ ![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,ABCD是菱形?
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB. 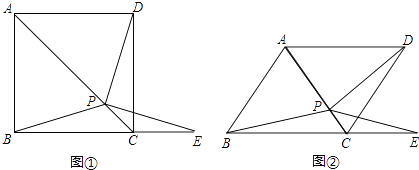
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地开辟一块长方形的荒地用于新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2,那么:
(1)荒地的宽是多少?有1 000 m吗?(结果保留一位小数)
(2)如果要求结果保留整数,那么宽大约是多少?
(3)计划在该公园中心建一个圆形花圃,面积是800 m2,你能估计它的半径吗?(要求结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90° 
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE ①求证:CD=DE;
②若sinA= ![]() ,AC=6,求AD.
,AC=6,求AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象; 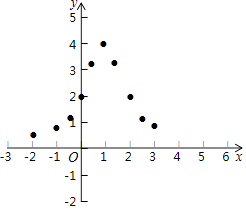
(4)结合函数图象,请写出函数y= ![]() 的一条性质.
的一条性质.
(5)解决问题:如果函数y= ![]() 与直线y=a的交点有2个,那么a的取值范围是 .
与直线y=a的交点有2个,那么a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com